
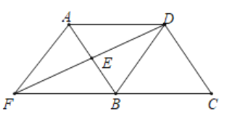
【题目】如图,已知在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,连结
的中点,连结![]() 并延长,与
并延长,与![]() 的延长线相交于点
的延长线相交于点![]() ,连结
,连结![]() .若
.若![]() ,
,![]() ,则四边形
,则四边形![]() 的面积是_________.
的面积是_________.
【答案】20
【解析】
由ASA证明△ADE≌△BFE,得出BF=AD,DE=FE,证出四边形AFBD是菱形,在Rt△BDE中,由三角函数得出DE=2BE,设BE=x,则DE=2x,由勾股定理得出方程,解方程求出![]() ,得出AB=2BE=2
,得出AB=2BE=2![]() ,DF=2DE=4BE=4
,DF=2DE=4BE=4![]() ,再由菱形面积公式即可得出结果.
,再由菱形面积公式即可得出结果.
∵四边形ABCD是平行四边形,
∴AD=BC=5,AB∥CD,AD∥BC,
∴∠BDC=∠DBE,∠ADE=∠BFE,
∵BD=BC=5,
∴AD=BD=5,
∵点E是AB的中点,
∴DE⊥AB,AE=BE,
∴AF=BF,
在△ADE和△BFE中,
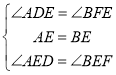 ,
,
∴△ADE≌△BFE(ASA),
∴BF=AD,DE=FE,
∴AD=BD=BF=AF,
∴四边形AFBD是菱形,
在Rt△BDE中,tan∠DBE=tan∠BDC=2,
∴![]() ,
,
∴DE=2BE,
设BE=![]() ,则DE=
,则DE=![]() ,
,
由勾股定理得:![]() +
+![]() =
=![]() ,即
,即![]() +
+![]() =
=![]() ,
,
解得:![]() ,
,
∴AB=2BE=2![]() ,DF=2DE=4BE=4
,DF=2DE=4BE=4![]() ,
,
∴四边形AFBD的面积=![]() ;
;
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等,交易其一,金轻十三两,问金、银一枚各重几何?”意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相同,两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计),问黄金、白银每枚各种多少两?设黄金重![]() 两,每枚白银重
两,每枚白银重![]() 两,根据题意可列方程组为____.
两,根据题意可列方程组为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若抛物线![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,直线
,直线![]() 经过点
经过点![]() ,
,![]() .
.
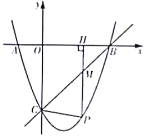
(1)求抛物线的解析式;
(2)点![]() 是直线
是直线![]() 下方抛物线上一动点,过点
下方抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
①线段![]() 是否有最大值?如果有,求出最大值;如果没有,请说明理由;
是否有最大值?如果有,求出最大值;如果没有,请说明理由;
②在点![]() 运动的过程中,是否存在点
运动的过程中,是否存在点![]() ,恰好使
,恰好使![]() 是以
是以![]() 为腰的等腰三角形?如果存在,请直接写出点
为腰的等腰三角形?如果存在,请直接写出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场第一次用11000元购进某款拼装机器人进行销售,很快销售一空,商家又用24000元第二次购进同款机器人,所购进数量是第一次的2倍,但单价贵了10元.
(1)求该商家第一次购进机器人多少个?
(2)若在这两次机器人的销售中,该商场全部售完,而且售价都是130元,问该商场总共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过![]() 上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
(1)求证:△ECF∽△GCE;
(2)求证:EG是⊙O的切线;
(3)延长AB交GE的延长线于点M,若tanG=![]() ,AH=
,AH=![]() ,求EM的值.
,求EM的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD;请证明你的结论.

【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(![]() ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据:
﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据: ![]() =1.41,
=1.41, ![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),则当售价x定为多少元时,厂商每天能获得最大利润?最大利润是多少?
(3)如果超市要获得每天不低于1350元的利润,且符合超市自己的规定,那么该商品每千克售价的取值范围是多少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
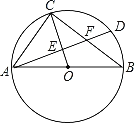
【题目】如图,△ABC内接于⊙O,AB为⊙O的直径,AB=10,AC=6,连结OC,弦AD分别交OC,BC于点E,F,其中点E是AD的中点.
(1)求证:∠CAD=∠CBA.
(2)求OE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com