
【题目】在![]() 中,
中,![]() ,点
,点![]() 是直线
是直线![]() 上一点(不与
上一点(不与![]() 、
、![]() 重合),以
重合),以![]() 为一边在
为一边在![]() 的右侧作
的右侧作![]() ,使
,使![]() ,
,![]() ,连接
,连接![]() .
.
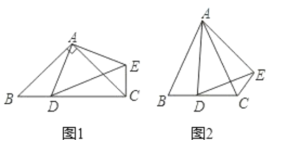
(1)如图1,当点![]() 在线段
在线段![]() 上时,如果
上时,如果![]() ,则
,则![]() ______度;
______度;
(2)设![]() ,
,![]() .
.
①如图2,当点![]() 在线段
在线段![]() 上移动,则
上移动,则![]() ,
,![]() 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;
②当点![]() 在直线
在直线![]() 上时,则
上时,则![]() ,
,![]() 之间有怎样的数量关系?
之间有怎样的数量关系?
写出所有可能的结论并说明条件.
答:(2)①数量关系____________.
理由:
②数量关系____________.
备用图:
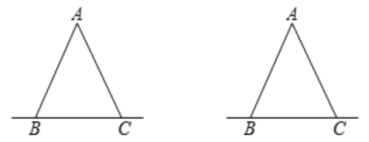
【答案】(1)90°;(2)①α+β=180°,理由见解析;②当点D在射线BC上时,α+β=180°;当点D在射线BC的反向延长线上时,α=β.
【解析】
(1)先用等式的性质得出∠CAE=∠BAD,再利用SAS判定△ABD≌△ACE,得到∠B=∠ACE,最后用等式的性质即可得出结论;
(2)①由(1)的结论即可得出α+β=180°;②分类讨论,同(1)的方法证明△ABD≌△ACE即可得出结论.
解:(1)∵∠BAC=∠DAE,
∴∠BAC∠DAC=∠DAE∠DAC,
即∠BAD=∠CAE,
在△ABD和△ACE中,
∵AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE(SAS);
∴∠B=∠ACE;
∴∠BCE=∠BCA+∠ACE=∠BCA+∠B=180°∠BAC=90°;
故答案为:90°;
(2)①由(1)的结论可知β=180°α,
∴α、β存在的数量关系为α+β=180°;
②当点D在射线BC上时,如图1,

同(1)的方法即可证△ABD≌△ACE(SAS);
∴∠ABD=∠ACE,
∴β=∠BCE=∠ACB+∠ACE=∠ACB+∠ABD=180°∠BAC=180°α,
∴α+β=180°;
当点D在射线BC的反向延长线上时,如图2,

同(1)的方法即可证△ABD≌△ACE(SAS);
∴∠ABD=∠ACE,
∴β=∠BCE=∠ACE∠ACB=∠ABD∠ACB=∠BAC=α,
∴α=β.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() 是常数)
是常数)
(1)求证:不论![]() 为何值,该函数图象与
为何值,该函数图象与![]() 轴一定有两个公共点。
轴一定有两个公共点。
(2)若该函数图象经过点(0,-2),则该函数图象怎样平移经过原点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习“分式”一章后,老师写出下面的一道题让同学们解答.
计算:![]() 其中小明的解答过程如下:
其中小明的解答过程如下:
解:原式 (A)
(A)
![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
(1)上述计算过程中,是从哪一步开始出现错误的?请写出该步代号:______;
(2)写出错误原因是____________;
(3)本题正确的解答过程.
解:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了发展学生的核心素养,培养学生的综合能力,某中学利用“阳光大课间”,组织学生积极参加丰富多彩的课外活动,学校成立了舞蹈队、足球队、篮球队、毽子队、射击队等,其中射击队在某次训练中,甲、乙两名队员各射击10发子弹,成绩记录如表:
射击次序(次) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲的成绩(环) | 8 | 9 | 7 | 9 | 8 | 6 | 7 | a | 10 | 8 |
乙的成绩(环) | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 | 7 | 10 |
(1)经计算甲和乙的平均成绩是8(环),请求出表中的a= ;
(2)甲成绩的中位数是 环,乙成绩的众数是 环;
(3)若甲成绩的方差是1.2,请求出乙成绩的方差,判断甲、乙两人谁的成绩更为稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接五一黄金周的购物高峰,某品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:
运动鞋价格 | 甲 | 乙 |
进价(元/双) | m | m﹣30 |
售价(元/双) | 240 | 160 |
已知:用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同.
(1)求m的值;
(2)若购进乙种运动鞋x(双),要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价﹣进价)不少于13000元且不超过13500元,问该专卖店有几种进货方案;
(3)在(2)的条件下求出总利润y(元)与购进乙种运动鞋x(双)的函数关系式,并用关系式说明哪种方案的利润最大,最大利润是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市某一城市美化工程招标时,有甲、乙两个工程队投标,经测算:甲队单独完成这项工程需要60天,若由甲队先做20天,剩下的工程由甲、乙合作24天可完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成工程省钱?还是由甲乙两队全程合作完成该工程省钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com