
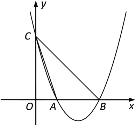
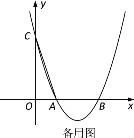
【题目】如图,抛物线![]() 交x轴于点
交x轴于点![]() 和点B,交y轴于点
和点B,交y轴于点![]() .
.
(1)求抛物线的解析式;
(2)在抛物线上找出点P,使![]() ,求点P的坐标;
,求点P的坐标;
(3)将直线AC沿x轴的正方向平移,平移后的直线交y轴于点M,交抛物线于点N.当四边形ACMN为等腰梯形时,求点M、N的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在M(0,
;(3)存在M(0,![]() )、N(
)、N(![]() ,-
,-![]() )使四边形ACMN为等腰梯形.
)使四边形ACMN为等腰梯形.
【解析】
(1)根据抛物线![]() 交x轴于点
交x轴于点![]() 和点B,交y轴于点
和点B,交y轴于点![]() .用待定系数法直接求出即可;
.用待定系数法直接求出即可;
(2)过P作![]() ,垂足为H,PO=OC,
,垂足为H,PO=OC,![]() ,则CH=OH
,则CH=OH![]() 令
令![]() ,解方程即可求出点P的横坐标,即可求解.
,解方程即可求出点P的横坐标,即可求解.
(3)连接NA并延长交OC于G,根据等腰梯形的性质得到GA=GC,设GA=x,则GC=x,OG=3-x在Rt△OGA中,根据勾股定理OA 2+OG 2=AG 2,列出方程,解得x= ![]()
∴OG=3-x=![]() ,求出 直线AG的解析式,联立方程,即可求出点N的坐标.进而求出点M的坐标.
,求出 直线AG的解析式,联立方程,即可求出点N的坐标.进而求出点M的坐标.
(1)∵抛物线![]() 过点A(1,0)、C(0,3)
过点A(1,0)、C(0,3)
∴![]()
解得 ![]()
∴抛物线的解析式为![]()
(2)过P作![]() ,垂足为H
,垂足为H
∵PO=OC,![]()
∴CH=OH![]()
∴ ![]() …
…
∴![]()
![]() .
.
(3)连接NA并延长交OC于G
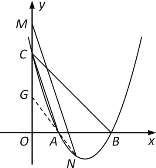
∵四边形ACMN为等腰梯形,且AC∥MN
∴∠ANM=∠CMN,∠ANM=∠GAC,∠GCA=∠CMN
∴∠GAC=∠GCA,∴GA=GC
设GA=x,则GC=x,OG=3-x
在Rt△OGA中,OA 2+OG 2=AG 2
∴1 2+( 3-x )2=x 2,解得x= ![]()
∴OG=3-x=![]() ,∴G(0,
,∴G(0,![]() )
)
易得直线AG的解析式为y=-![]() x+
x+![]()
令- ![]() x+
x+ ![]() =x 2-4x+3,解得x1=1(舍去),x2=
=x 2-4x+3,解得x1=1(舍去),x2= ![]()
∴N![]()
∴CM=AN=![]()
∴OM=OC+CM=3+ ![]() =
= ![]()
∴M(0,![]() )
)
∴存在M(0,![]() )、N
)、N![]() 使四边形ACMN为等腰梯形
使四边形ACMN为等腰梯形


科目:初中数学 来源: 题型:
【题目】下面是小星同学设计的“过直线外一点作已知直线的平行线”的尺规作图过程:
已知:如图,直线 l 和直线 l 外一点 A
求作:直线 AP,使得 AP∥l
作法:如图
① 在直线 l 上任取一点 B,以点 A 为圆心,AB 为半径作圆,与直线 l 交于 B,C 两点.
② 连接 AC,AB,延长 BA 交⊙A 于点 D;
③ 作∠DAC 的平分线 AP,并反向延长.
所以直线 AP 就是所求作的直线
根据小星同学设计的尺规作图过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹)
(2)完成下面的证明
证明:∵AB=AC,
∴∠ABC=∠ACB( ① )(填推理的依据)
∵∠DAC 是△ABC 的外角,
∴∠DAC=∠ABC+∠ACB
∴∠DAC=2∠ABC
∵AP 平分∠DAC,
∴∠DAC=2∠DAP
∴ ②
∴AP∥l( ③ )(填推理的依据)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=ax2+bx+c(a≠0)的顶点坐标A(﹣1,3),与x轴的一个交点B(﹣4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①2a﹣b=0;②abc<0;③抛物线与x轴的另一个交点坐标是(3,0);④方程ax2+bx+c﹣3=0有两个相等的实数根;⑤当﹣4<x<﹣1时,则y2<y1.
其中正确的是( )

A. ①②③ B. ①③⑤ C. ①④⑤ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,BC=3,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H,求BDcos∠HBD的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当四边形MENF是正方形时,求AD:AB的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=x2+bx+c(c≠0)的图象经过点A(-2,m)(m<0),与y轴交于点B,与x轴交于C、D两点(C在D的左侧),AB//x轴,且AB:OB=2:3.
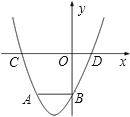
(1)求m的值;
(2)求二次函数的解析式;
(3)在线段BC上是否存在点P,使ΔPOC为等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次函数y=kx-6中,已知y随x的增大而减小.下列关于反比例函数y=![]()
的描述,其中正确的是( )
A. 当x>0时,y>0 B. y随x的增大而增大
C. y随x的增大而减小 D. 图像在第二、四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
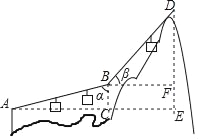
【题目】如图,游客在点A处坐缆车出发,沿A﹣B﹣D的路线可至山顶D处.已知AB=BD=800米,∠α=75°,∠β=45°,求山高DE(结果精确到1米).(参考数据:sin75°=0.966,cos75°=0.259,tan75°=3.732,![]() =1.414)
=1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
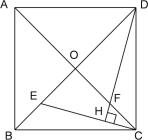
【题目】已知:如图,菱形ABCD的对角线AC与BD相交于点O,若∠CAD=∠DBC.
(1)求证:ABCD是正方形.
(2)E是OB上一点,DH⊥CE,垂足为H,DH与OC相交于点F,求证:OE=OF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com