
【题目】因2019年下半年猪肉大涨,某养猪专业户想扩大养猪场地,但为了节省材料,利用一面墙(墙足够长)为一边,用总长为120![]() 的材料围成了如图所示①②③三块矩形区域,而且这三块矩形区域的面积相等,设
的材料围成了如图所示①②③三块矩形区域,而且这三块矩形区域的面积相等,设![]() 的长度为
的长度为![]() (
(![]() ),矩形区域
),矩形区域![]() 的面积
的面积![]() (
(![]() ).
).
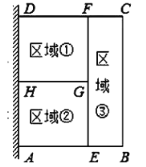
(1)求![]() 与
与![]() 之间的函数表达式,并注明自变量
之间的函数表达式,并注明自变量![]() 的取值范围.
的取值范围.
(2)当![]() 为何值时,
为何值时,![]() 有最大值?最大值是多少?
有最大值?最大值是多少?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
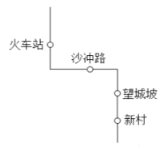
【题目】2018年12月1日,贵阳地铁一号线正式开通,标志着贵阳中心城区正式步入地铁时代,为市民的出行带来了便捷,如图是贵阳地铁一号线路图(部分),菁菁与琪琪随机从这几个站购票出发.
(1)菁菁正好选择沙冲路站出发的概率为
(2)用列表或画树状图的方法,求菁菁与琪琪出发的站恰好相邻的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
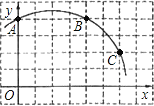
【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1)在图中确定该圆弧所在圆的圆心D点的位置,并写出点D点坐标为________.
(2)连接AD、CD,求⊙D的半径及![]() 的长;
的长;
(3)有一点E(6,0),判断点E与⊙D的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=﹣2.关于下列结论:①ab<0;②b2﹣4ac>0;③9a﹣3b+c>0;④b﹣4a=0;⑤ 方程ax2+bx=0的两个根为 x1=0,x2=﹣4,其中正确的结论有( )
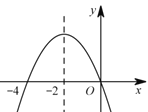
A.②③B.②③④C.②③⑤D.②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,AD=3,点E是边CD的中点,点P,Q分别是射线DC与射线EB上的动点,连结PQ,AP,BP,设DP=t,EQ=![]() t.
t.
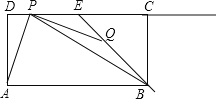
(1)当点P在线段DE上(不包括端点)时.
①求证:AP=PQ;②当AP平分∠DPB时,求△PBQ的面积.
(2)在点P,Q的运动过程中,是否存在这样的t,使得△PBQ为等腰三角形?若存在,请求出t的值;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,点D、点E分别在边AB、AC上,且DE // BC,BE平分∠ABC.
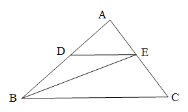
(1)求证:BD=DE;
(2)若AB=10,AD=4,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙O的半径为r(r>0).给出如下定义:若平面上一点P到圆心O的距离d,满足![]() ,则称点P为⊙O的“随心点”.
,则称点P为⊙O的“随心点”.
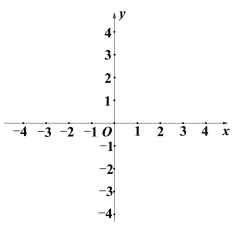
(1)当⊙O的半径r=2时,A(3,0),B(0,4),C(![]() ,2),D(
,2),D(![]() ,
,![]() )中,⊙O的“随心点”是 ;
)中,⊙O的“随心点”是 ;
(2)若点E(4,3)是⊙O的“随心点”,求⊙O的半径r的取值范围;
(3)当⊙O的半径r=2时,直线y=- x+b(b≠0)与x轴交于点M,与y轴交于点N,若线段MN上存在⊙O的“随心点”,直接写出b的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司对自家办公大楼一块![]() 米的正方形墙面进行了如图所示的设计装修(四周阴影部分是八个全等的矩形,用材料甲装修;中心区是正方形
米的正方形墙面进行了如图所示的设计装修(四周阴影部分是八个全等的矩形,用材料甲装修;中心区是正方形![]() ,用材料乙装修). 两种材料的成本如下表:
,用材料乙装修). 两种材料的成本如下表:

材料 | 甲 | 乙 |
价格(元/米2) | 550 | 500 |
设矩形的较短边![]() 的长为
的长为![]() 米,装修材料的总费用为
米,装修材料的总费用为![]() 元.
元.
(1)计算中心区的边![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(2)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)当中心区的边长![]() 不小于2米时,预备材料的购买资金32000元够用吗?请利用函数的增减性来说明理由.
不小于2米时,预备材料的购买资金32000元够用吗?请利用函数的增减性来说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知某小区的两幢10层住宅楼间的距离为AC="30" m,由地面向上依次为第1层、第2层、…、第10层,每层高度为3 m.假设某一时刻甲楼在乙楼侧面的影长EC=h,太阳光线与水平线的夹角为α .
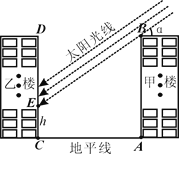
(1) 用含α的式子表示h(不必指出α的取值范围);
(2) 当α=30°时,甲楼楼顶B点的影子落在乙楼的第几层?若α每小时增加15°,从此时起几小时后甲楼的影子刚好不影响乙楼采光 ?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com