
分析 当k=1时,直线解析式为y=x和y=2x+1,利用两直线相交的问题求出它们的交点坐标为(-1,-1),再分别求出它们与x轴的交点坐标,然后根据三角形面积公式计算出S1=$\frac{1}{2}$×$\frac{1}{1×2}$,利用同样方法可得到S2=$\frac{1}{2}$×$\frac{1}{2×3}$,S3=$\frac{1}{2}$×$\frac{1}{3×4}$,利用这三个数的规律可得到Sk=$\frac{1}{2}$×$\frac{1}{k(k+1)}$,则S10=$\frac{1}{2}$×$\frac{1}{10×11}$,然后利用$\frac{1}{k(k+1)}$=$\frac{1}{k}$-$\frac{1}{k+1}$计算S1+S2+S3+…+S10的值.
解答 解:当k=1时,直线y=x与直线y=2x+1的交点坐标为(-1,-1),直线y=x与x轴的交点坐标为(0,0),直线y=2x+1与x轴的交点为(-$\frac{1}{2}$,0),所以S1=$\frac{1}{2}$•$\frac{1}{2}$•1=$\frac{1}{2}$×$\frac{1}{2}$=$\frac{1}{2}$×$\frac{1}{1×2}$;
当k=2时,直线y=2x+1与直线y=3x+2的交点坐标为(-1,-1),直线y=2x+1与x轴的交点为(-$\frac{1}{2}$,0),直线y=3x+2与x轴的交点为(-$\frac{2}{3}$,0),所以S2=$\frac{1}{2}$•(-$\frac{1}{2}$+$\frac{2}{3}$)•1=$\frac{1}{2}$×$\frac{1}{2×3}$;
当k=3时,直线y=3x+2与直线y=4x+3的交点坐标为(-1,-1),直线y=3x+2与x轴的交点为(-$\frac{2}{3}$,0),直线y=4x+3与x轴的交点为(-$\frac{3}{4}$,0),所以S3=$\frac{1}{2}$•(-$\frac{2}{3}$+$\frac{3}{4}$)•1=$\frac{1}{2}$×$\frac{1}{12}$=$\frac{1}{2}$×$\frac{1}{3×4}$;
所以S10=$\frac{1}{2}$×$\frac{1}{10×11}$,
所以S1+S2+S3+…+S10=$\frac{1}{2}$×$\frac{1}{1×2}$+$\frac{1}{2}$×$\frac{1}{2×3}$+$\frac{1}{2}$×$\frac{1}{3×4}$+…+$\frac{1}{2}$×$\frac{1}{10×11}$=$\frac{1}{2}$(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{10}$-$\frac{1}{11}$)=$\frac{1}{2}$×(1-$\frac{1}{11}$)=$\frac{5}{11}$.
故答案为$\frac{5}{11}$.
点评 本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.计算S1、S2、S3的值,从中找到Sk的规律是解决本题的关键.


科目:初中数学 来源: 题型:填空题
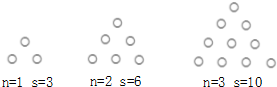 如图所示每个图形是由若干个花盆组成的三角形的图案,每条边(包括顶点)有n(n>1)盆花,每个图案共有s盆花,则s与n之间的关系式为s=$\frac{(n+1)(n+2)}{2}$.
如图所示每个图形是由若干个花盆组成的三角形的图案,每条边(包括顶点)有n(n>1)盆花,每个图案共有s盆花,则s与n之间的关系式为s=$\frac{(n+1)(n+2)}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com