Question

15．（1）在图中每个小方格内填入一个数，使每一行、每一列都有1、2、3、4、5，那么，右上角的小方格内填入x的数应是1．
（2）已知数据$\frac{1}{3}$，$\frac{2}{5}$，$\frac{3}{7}$，$\frac{4}{9}$，…第（n+1）个是$\frac{n+1}{2n+3}$．

Answer 1

分析 （1）按照图形，首先补充多数字的行或列，在各方格中填入数字，每一行每一列都有1-5数字；
（2）根据已知，可以发现分数分子和序号相同，分母是序号的2倍加1，由此可以求出第（n+1）个数．

解答 解：（1）将图形补充完整，如下图：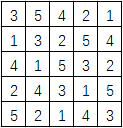

故右上角的小方格内填入x的数应是1．
故答案为：1．

（2）根据已知：
第1个数：$\frac{1}{3}$=$\frac{1}{2×1+1}$，
第2个数：$\frac{2}{5}$=$\frac{2}{2×2+1}$，
第3个数：$\frac{3}{7}$=$\frac{3}{2×3+1}$，
第4个数：$\frac{4}{9}=\frac{4}{2×4+1}$，
…，
故第（n+1）个数：$\frac{n+1}{2×（n+1）+1}$=$\frac{n+1}{2n+3}$．
故答案为：$\frac{n+1}{2n+3}$．

点评 题目考查了数字的变化规律，解决此类问题的关键是找出所求数字与序号的关系，题目整体较为简单，适合随堂训练．