
 我们曾经通过列表、画图象,研究了函数y=ax2(a≠0)的性质,知道它的图象是一条抛物线,通过图象还研究了它的相关性质;经过平移函数y=ax2(a≠0)的图象还可得到函数y=a(x-h)2+k,(a≠0)的图象.用类似的方法还可研究其他函数的有关性质.
我们曾经通过列表、画图象,研究了函数y=ax2(a≠0)的性质,知道它的图象是一条抛物线,通过图象还研究了它的相关性质;经过平移函数y=ax2(a≠0)的图象还可得到函数y=a(x-h)2+k,(a≠0)的图象.用类似的方法还可研究其他函数的有关性质.| x | … | -2 | -1 | 0 | 1 | 2 | … | ||
| y | … | 0 | 4 | … |
分析 (1)利用已知函数解析式进而计算得出答案;
(2)利用(1)中所求数据描点连线即可;
(3)①利用函数图象即可得出对称性;
②利用函数图象得出增减性;
③利用函数图象得出有没有最值;
④利用函数平移的性质,左加右减,上加下减即可得出答案.
解答 解:(1)填表如下:
| x | … | -2 | -1 | -$\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 1 | 2 | … |
| y | … | -4 | -$\frac{1}{2}$ | -$\frac{1}{16}$ | 0 | $\frac{1}{16}$ | $\frac{1}{2}$ | 4 | … |
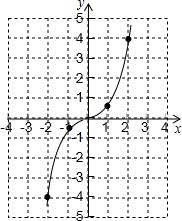
点评 此题主要考查了函数问题综合以及函数增减性以及其对称性、最值平移规律等知识,结合已知函数解析式画出图象是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
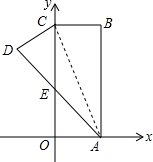 如图,在直角坐标系中,长方形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(2,6),将长方形沿对角线AC翻折,点B落在点D的位置,且AD交y轴于点E,则点D的坐标为(-$\frac{8}{5}$,$\frac{24}{5}$).
如图,在直角坐标系中,长方形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(2,6),将长方形沿对角线AC翻折,点B落在点D的位置,且AD交y轴于点E,则点D的坐标为(-$\frac{8}{5}$,$\frac{24}{5}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com