
【题目】小华是数学兴趣小组的一名成员,他在学过二次函数的图像与性质之后,对![]() 的图像与性质进行了探究,探究过程如下,请你补充完整.
的图像与性质进行了探究,探究过程如下,请你补充完整.
(1)小刚通过计算得到几组对应的数值如下
| … |
|
|
|
|
|
| 0 | 1 |
| 2 | 3 | 4 | 5 | … |
| … |
| 0 | 4 | 6 |
| 6 | 4 | 6 |
| 6 | 4 | 0 |
| … |
填空:自变量的取值范围是__________________,![]() __________.
__________.
(2)在如图所示的平面直角坐标系中,描出上表中各组对应数值的点,并根据描出的点,画出该函数的图像.
(3)请你根据画出的图像,写出此函数的两条性质;
①__________________________________________;
②__________________________________________.
(4)直线![]() 经过
经过![]() ,若关于
,若关于![]() 的方程
的方程![]() 有4个不相等的实数根,则
有4个不相等的实数根,则![]() 的取值范围为_________.
的取值范围为_________.

【答案】(1)全体实数,-6;(2)见解析;(3)①该函数的图象关于![]() 轴对称;②函数的图象有最高点;(4)
轴对称;②函数的图象有最高点;(4)![]()
【解析】
(1)因为此函数表达式为整式,所以自变量取值范围为全体实数,由表格可观察出函数关于y轴对称,x=-5时,y=-6,所以x=5时,y=-6,进而得出a的值;
(2)描出表中各组对应数值的点,再用平滑的曲线连接即可;
(3)观察可得出①该函数的图象关于![]() 轴对称,②函数的图象有最高点(答案不唯一);
轴对称,②函数的图象有最高点(答案不唯一);
(4)方程![]() 的根的个数在图像上表现为函数
的根的个数在图像上表现为函数![]() 与
与![]() 的交点个数,作出符合四个交点的情况,即可得出b的取值范围.
的交点个数,作出符合四个交点的情况,即可得出b的取值范围.
(1)因为此函数表达式为整式,所以自变量取值范围为全体实数;
由表格可观察出函数关于y轴对称,x=-5时,y=-6,所以x=5时,y=-6,即a=-6;
故答案为:全体实数,-6;
(2)如图所示
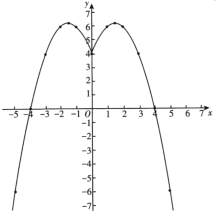
(3)①该函数的图象关于![]() 轴对称
轴对称
②函数的图象有最高点(答案不唯一)
(4)当x<0时,函数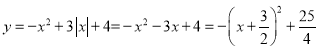 ,
,
∴左侧最高点为![]() ,
,
∵函数关于y轴对称,
∴右侧最高点为![]()
∴当直线经过两个最高点,如下图所示,直线与该函数有两个不同的交点,
此时,k=0,b=![]()
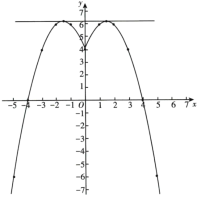
当直线经过(0,4)时,b=4,此时直线与该函数有3个交点,如下图所示,
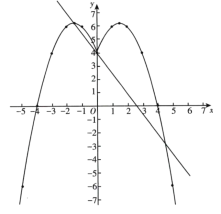
由上述两种情况可知,当b在4到![]() 之间时,直线与该函数图象会有4个交点,即关于
之间时,直线与该函数图象会有4个交点,即关于![]() 的方程
的方程![]() 有4个不相等的实数根,
有4个不相等的实数根,
∴b的取值范围为![]() .
.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在某场足球比赛中,球员甲从球门底部中心点![]() 的正前方
的正前方![]() 处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为
处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为![]() 时达到最高点,此时足球飞行的水平距离为
时达到最高点,此时足球飞行的水平距离为![]() .已知球门的横梁高
.已知球门的横梁高![]() 为
为![]() .
.

![]() 在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)
在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)
![]() 守门员乙站在距离球门
守门员乙站在距离球门![]() 处,他跳起时手的最大摸高为
处,他跳起时手的最大摸高为![]() ,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?
,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?
查看答案和解析>>
科目:初中数学 来源: 题型:
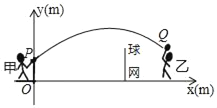
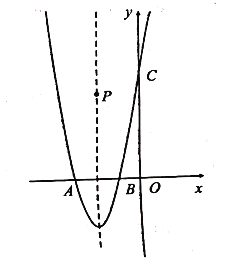
【题目】甲、乙两人进行羽毛球比赛,把球看成点,其飞行的路线为抛物线的一部分.如图建立平面直角坐标系,甲在O点正上方1m的P处发球,羽毛球飞行的高度y(m)与羽毛球距离甲站立位置(点O)的水平距离x(m)之间满足函败表达式y=a(x﹣4)2+h.已知点O与球网的水平距离为5m,球网的高度为1.55m,球场边界距点O的水平距离为10m.
(1)当a=﹣![]() 时,求h的值,并通过计算判断此球能否过网.
时,求h的值,并通过计算判断此球能否过网.
(2)若甲发球过网后,乙在另一侧距球网水平距离lm处起跳扣球没有成功,球在距球网水平距离lm,离地面高度2.2m处飞过,通过计算判断此球会不会出界?
查看答案和解析>>
科目:初中数学 来源: 题型:
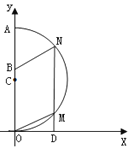
【题目】如图,在平面直角坐标系中,平行四边形BOMN的一边延长线交x轴于点D,OB=18,OD=12,点C为线段BO上一点,以C点为圆心,CO为半径的圆过M、N两点,且与y轴交于点A,则OA长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
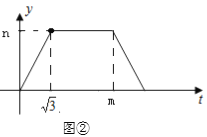
【题目】如图,在平行四边形ABCD中,∠D=60°,点M在线段AD上,DM= ![]() ,AM=2,点E从点D出发,沿着D-C-B-A匀速运动,速度为每秒2个单位长度,达到A点后停止运动,设△MDE的面积为y,点E运动的时间为t(s),y与t的部分函数关系如图②所示.
,AM=2,点E从点D出发,沿着D-C-B-A匀速运动,速度为每秒2个单位长度,达到A点后停止运动,设△MDE的面积为y,点E运动的时间为t(s),y与t的部分函数关系如图②所示.
(1)如图①中,DC=_____,如图②中,m=_______,n=_____.
(2)在E点运动过程中,将平行四边形沿ME所在直线折叠,则t为何值时,折叠后顶点D的对应点D′落在平行四边形的一边上.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场在“五一”促销活动中规定,顾客每消费100元就能获得一次中奖机会.为了活跃气氛.设计了两个抽奖方案:
方案一:转动转盘![]() 一次,转出红色可领取一份奖品;
一次,转出红色可领取一份奖品;
方案二:转动转盘![]() 两次,两次都转出红色可领取一份奖品.(两个转盘都被平均分成3份)
两次,两次都转出红色可领取一份奖品.(两个转盘都被平均分成3份)
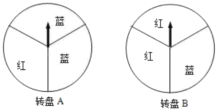
(1)若转动一次![]() 转盘,求领取一份奖品的概率;
转盘,求领取一份奖品的概率;
(2)如果你获得一次抽奖机会,你会选择哪个方案?请采用列表法或树状图说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .
.
(1)求点![]() ,点
,点![]() 的坐标;
的坐标;
(2)我们规定:对于直线![]() ,直线
,直线![]() ,若
,若![]() ,则直线
,则直线![]() ;反过来也成立.请根据这个规定解决下列问题:
;反过来也成立.请根据这个规定解决下列问题:
①直线![]() 与直线
与直线![]() 是否垂直?并说明理由;
是否垂直?并说明理由;
②若点![]() 是抛物线
是抛物线![]() 的对称轴上一动点,是否存在点
的对称轴上一动点,是否存在点![]() 与点
与点![]() ,点
,点![]() 构成以
构成以![]() 为直角边的直角三角形?若存在,请求出点
为直角边的直角三角形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD内一点,点P到点A,B和D的距离分别为1,2![]() ,
,![]() .△ADP沿点A旋转至△ABP′,连接PP′,并延长AP与BC相交于点Q.
.△ADP沿点A旋转至△ABP′,连接PP′,并延长AP与BC相交于点Q.
(1)求证:△APP′是等腰直角三角形;
(2)求∠BPQ的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=90°,A是∠MON内部的一点,过点A作AB⊥ON,垂足为点B,AB=3厘米,OB=4厘米,动点E、F同时从O点出发,点E以1.5厘米/秒的速度沿ON方向运动,点F以2厘米/秒的速度沿OM方向运动,EF与OA交于点C,连接AE,当点E到达点B时,点F随之停止运动,设运动时间为t秒(t>0).
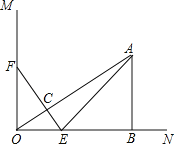
(1)当t=1秒时,△EOF与△ABO是否相似?请说明理由;
(2)在运动过程中,不论t取何值,总有EF⊥OA,为什么?
(3)在运动过程中,是否存在某一时刻t,使得△AEB与△OEF相似?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com