
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |


科目:初中数学 来源: 题型:
 如图,△ABC中,AB=AC,BD平分∠ABC交AC于G,DM∥BC交∠ABC的外角平分线于M,交AB,AC于F,E,以下结论:①MB⊥BD,②FD=EC,③EC=EF+DG,④CE=
如图,△ABC中,AB=AC,BD平分∠ABC交AC于G,DM∥BC交∠ABC的外角平分线于M,交AB,AC于F,E,以下结论:①MB⊥BD,②FD=EC,③EC=EF+DG,④CE=| 1 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 听说中考要考尺规作图,一天,老师在黑板上画了两条线段(如图),要求“以a为底、b为底边上的高,用尺规作一个等腰三角形,并写出已知和求作”.初三的小明早已生疏尺规作图了,请聪明的你帮帮他.
听说中考要考尺规作图,一天,老师在黑板上画了两条线段(如图),要求“以a为底、b为底边上的高,用尺规作一个等腰三角形,并写出已知和求作”.初三的小明早已生疏尺规作图了,请聪明的你帮帮他.查看答案和解析>>
科目:初中数学 来源: 题型:

| A、4n+6,n(n+1) |
| B、4n+6,n(n+2) |
| C、n(n+1),4n+6 |
| D、n(n+2),4n+6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
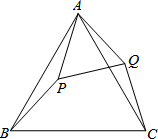 如图,等边△ABC,点P在△ABC内,点Q在△ABC外,分别联结AP、BP、AQ、CQ,∠ABP=∠ACQ,BP=CQ.
如图,等边△ABC,点P在△ABC内,点Q在△ABC外,分别联结AP、BP、AQ、CQ,∠ABP=∠ACQ,BP=CQ.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com