
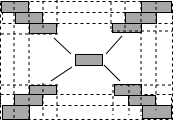
 如图,某广场的休闲区由1×1的小正方形瓷砖无空隙地铺成长方形,若该休闲区黑色小正方形共有82块,则白色小正方形的块数是( )
如图,某广场的休闲区由1×1的小正方形瓷砖无空隙地铺成长方形,若该休闲区黑色小正方形共有82块,则白色小正方形的块数是( )| A. | 340 | B. | 380 | C. | 402 | D. | 424 |
分析 此题可以看做是实心方阵问题,要求白色小正方形的块数,只要求出总块数即可得解,然后根据该休闲区黑色小正方形共有82块,可得每条对角线上的块数为:(82+2)÷4=21(块),所以这个实心方阵的每条边有21+1=22(块)小正方形,据此求出小正方形瓷砖的总块数,再用小正方形瓷砖的总块数减去该休闲区黑色小正方形的数量,求出白色小正方形的块数是多少即可.
解答 解:(82+2)÷4=21(块)
白色小正方形的块数是:
(21+1)×(21+1)-82
=22×22-82
=484-82
=402(块)
故选:C.
点评 此题主要考查了规律型:图形的变化类问题,首先应找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.探寻规律要认真观察、仔细思考,善用联想来解决这类问题,解答此题的关键是要明确:方阵的总点数=每边的点数×每边的点数.


科目:初中数学 来源: 题型:解答题
| 品名 | 黄瓜 | 茄子 |
| 批发价(元/千克) | 3 | 4 |
| 零售价(元/千克) | 4 | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
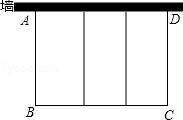 如图,孔明想利用一面长为45米的墙建羊圈,用100米的围栏围成总面积为600平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米?孔明能在原来的基础上建一个面积为640平方米的羊圈吗?说说理由.
如图,孔明想利用一面长为45米的墙建羊圈,用100米的围栏围成总面积为600平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米?孔明能在原来的基础上建一个面积为640平方米的羊圈吗?说说理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
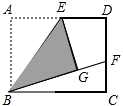 (1)如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=1,FD=2,则BC的长为2$\sqrt{6}$.
(1)如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=1,FD=2,则BC的长为2$\sqrt{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
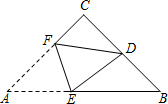 如图,△ABC中,∠C=90°,AC=BC,点D为BC的中点,将△ABC折叠,使点A与点D重合,EF为折痕,则tan∠BED的值为$\frac{3}{4}$.
如图,△ABC中,∠C=90°,AC=BC,点D为BC的中点,将△ABC折叠,使点A与点D重合,EF为折痕,则tan∠BED的值为$\frac{3}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4对 | B. | 6对 | C. | 8对 | D. | 9对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com