
分析 (1)假设购进A种树苗x棵,则购进B种树苗(17-x)棵,利用购进A、B两种树苗刚好用去1220元,结合单价,得出等式方程求出即可;
(2)根据所需费用为W=A种树苗的费用+B种树苗的费用,即可解答;
(3)结合(1)的解和购买B种树苗的数量少于A种树苗的数量,可找出方案.
解答 解:(1)设购进A种树苗x棵,则购进B种树苗(17-x)棵,根据题意得:
80x+60(17-x )=1220,
解得:x=10,
∴17-x=7,
答:购进A种树苗10棵,B种树苗7棵;
(2)购进a种树苗A棵,则购进B种树苗(17-a)棵
根据题意得:W=80a+60(17-a)=20a+1020.
(3)∵购买B种树苗的数量少于A中树苗的数量,
∴17-a<a,
解得:a>8$\frac{1}{2}$.
购进A、B两种树苗所需费用为W=20a+1020,
因为A种树苗贵,则费用最省需x取最小整数9,
此时17-a=8,
这时所需费用为20×9+1020=1200(元).
答:费用最省方案为:购进A种树苗9棵,B种树苗8棵.这时所需费用为1200元.
点评 此题主要考查了一元一次不等式组的应用以及一元一次方程应用,根据一次函数的增减性得出费用最省方案是解决问题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
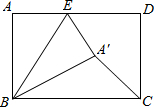 如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰好落在∠BCD 的平分线上时,CA1的长为( )
如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰好落在∠BCD 的平分线上时,CA1的长为( )| A. | 3或4$\sqrt{2}$ | B. | 4或3$\sqrt{2}$ | C. | 3或4 | D. | 3$\sqrt{2}$或4$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
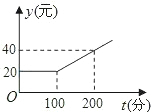 有甲、乙两家通迅公司,甲公司每月通话的收费标准如图所示;乙公司每月通话收费标准如表所示:
有甲、乙两家通迅公司,甲公司每月通话的收费标准如图所示;乙公司每月通话收费标准如表所示:| 月租费 | 通话费 |
| 25元 | 0.15元/分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
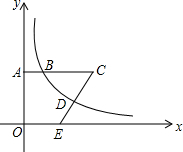 如图所示的平面直角坐标系xOy,点A在y轴正半轴上运动,点B在第一象限,AB⊥y轴,AB=4,在AB的延长点上取一点C,过点C作直线交过点B的双曲线于点D,交x轴正半轴于点E,且CD=DE,设OA=t,四边形OACE的面积为S.
如图所示的平面直角坐标系xOy,点A在y轴正半轴上运动,点B在第一象限,AB⊥y轴,AB=4,在AB的延长点上取一点C,过点C作直线交过点B的双曲线于点D,交x轴正半轴于点E,且CD=DE,设OA=t,四边形OACE的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
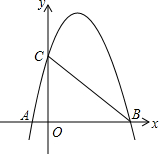 如图,抛物线与x轴相交于A(-1,0),B(3,0)两点,与y轴相交于点C(0,3).
如图,抛物线与x轴相交于A(-1,0),B(3,0)两点,与y轴相交于点C(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
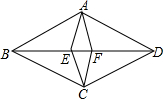 如图,四边形ABCD与四边形AECF都是菱形,点E、F在BD上.已知∠BAD=120°,∠EAF=30°,则$\frac{AB}{AE}$=$\frac{\sqrt{6}+\sqrt{2}}{2}$.
如图,四边形ABCD与四边形AECF都是菱形,点E、F在BD上.已知∠BAD=120°,∠EAF=30°,则$\frac{AB}{AE}$=$\frac{\sqrt{6}+\sqrt{2}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com