

 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:初中数学 来源: 题型:解答题
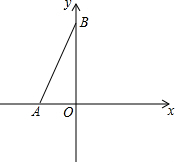 如图,在平面直角坐标系中,A(a,0),B(0,b),且a,b满足|a+b-4|+(2a+4)2=0.
如图,在平面直角坐标系中,A(a,0),B(0,b),且a,b满足|a+b-4|+(2a+4)2=0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 尺规作图(请保留作图痕迹,不写作法).
尺规作图(请保留作图痕迹,不写作法).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | 9 | C. | 1 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
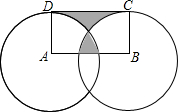 如图,分别以矩形ABCD的顶点A和B为圆心,作半径为1的两个圆正好分别经过C、D两点,若图中两块阴影部分的面积相等,则AB的长度是$\frac{π}{2}$.
如图,分别以矩形ABCD的顶点A和B为圆心,作半径为1的两个圆正好分别经过C、D两点,若图中两块阴影部分的面积相等,则AB的长度是$\frac{π}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
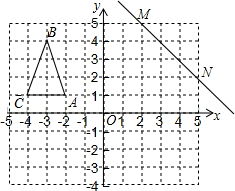 如图,在直角坐标系中有一个格点三角形ABC(顶点都在格点上的三角形),已知A(-2,1),B(-3,4),C(-4,1),直线MN过点M(2,5),N(5,2).
如图,在直角坐标系中有一个格点三角形ABC(顶点都在格点上的三角形),已知A(-2,1),B(-3,4),C(-4,1),直线MN过点M(2,5),N(5,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
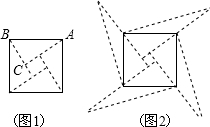 图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中的边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( )
图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中的边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( )| A. | 51 | B. | 49 | C. | 76 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com