
分析 我们把两只蚂蚁按原速爬行称为第一次爬行,把提高速度后的爬行称为第二次爬行,第一次爬行时,两只蚂蚁的速度和是每分钟600÷15=40(米).第二次爬行时,两只蚂蚁的速度和是每分钟40+5×2=50(米),需要经过600÷50=12(分)相遇;第二次在距第一次相遇点15米的地方相遇,即第二次两只蚂蚁爬行的路程之差比第一次少15×2=30(米),又因为第二次爬行两只蚂蚁的速度都提高了5米,即它们的速度之差是不变的,所以相差的30米路程是两只蚂蚁爬行(15-12)分钟的路程之差,由此可求出两只蚂蚁的速度之差是30÷(15-12)=10(米).则甲蚂蚁原来每分钟爬行(40+10)÷2=25(米),乙蚂蚁原来每分钟爬行(40-10)÷2=15(米),再用路程除以甲蚂蚁的速度就可以求出甲蚂蚁从A地爬到B地需要多少分钟.
解答 解:两只蚂蚁原来的速度和为:600÷15=40(米/分),
现在的速度和为:40+2×5=50(米/分),
相遇时间为:600÷50=12(分),
速度差为:15×2÷(15-12)=10(米),
甲蚂蚁的速度为:(40+10)÷2=25(米/分),
600÷25=24(分)
答:甲蚂蚁从A爬到B地需要24分钟.
点评 本题主要考查相遇问题的实际应用,解答本题的关键是根据路程差求出速度差,从而求出两只蚂蚁的速度.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:解答题
 有一座小型三塘的塘坝横截面是一个等腰梯形,上底宽为1.2米,坡长为3米,坡度i=$\sqrt{3}:1$,求塘坝的横截面积.($\sqrt{3}$=1.732,计算结果精确到0.01)
有一座小型三塘的塘坝横截面是一个等腰梯形,上底宽为1.2米,坡长为3米,坡度i=$\sqrt{3}:1$,求塘坝的横截面积.($\sqrt{3}$=1.732,计算结果精确到0.01)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
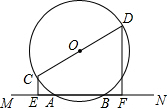 如图,直线MN与⊙O相交于点A、B,CD是直径,CE⊥MN于E,DF⊥MN于F,求证:
如图,直线MN与⊙O相交于点A、B,CD是直径,CE⊥MN于E,DF⊥MN于F,求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
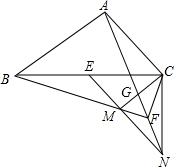 如图,在四边形ABFC中,∠BAC=∠BFC=∠BCN=90°,E为BC中点,过C作CN⊥BC交AF于N点,连接EN交BF于M点,连接CM交AN于G点,若AB=AF,求证:MG=GC.
如图,在四边形ABFC中,∠BAC=∠BFC=∠BCN=90°,E为BC中点,过C作CN⊥BC交AF于N点,连接EN交BF于M点,连接CM交AN于G点,若AB=AF,求证:MG=GC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在直角梯形ABCD中,AB∥CD,∠BCD=RT∠,AB=AD=10cm,BC=8cm,点P从点A出发,以每秒3cm的速度沿直线ABCD方向运动,点Q从点D出发以每秒2cm的速度沿线段DC方向向点C运动,已知动点P,Q同时出发,当点Q运动到点C时,P,Q运动停止,设运动时间为t.
在直角梯形ABCD中,AB∥CD,∠BCD=RT∠,AB=AD=10cm,BC=8cm,点P从点A出发,以每秒3cm的速度沿直线ABCD方向运动,点Q从点D出发以每秒2cm的速度沿线段DC方向向点C运动,已知动点P,Q同时出发,当点Q运动到点C时,P,Q运动停止,设运动时间为t.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com