Question

1．如图，从地面上的点A看一山坡上的电线杆PQ，测得杆顶端点P的仰角是45°，向前走9m到达B点，测得杆顶端点P和杆底端点Q的仰角分别是60°和30°．
（1）求∠BPQ的度数；
（2）求该电线杆PQ的高度．（结果保留根号）

Answer 1

分析 （1）延长PQ交直线AB于点E，根据直角三角形两锐角互余求得即可；
（2）设PE=x米，在直角△APE和直角△BPE中，根据三角函数利用x表示出AE和BE，根据AB=AE-BE即可列出方程求得x的值，再在直角△BQE中利用三角函数求得QE的长，则PQ的长度即可求解．

解答 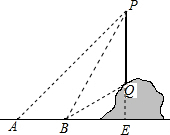解：延长PQ交直线AB于点E，如图所示：
（1）∠BPQ=90°-60°=30°；
（2）设PE=x米．
在直角△APE中，∠A=45°，
则AE=PE=x米；
∵∠PBE=60°，
∴∠BPE=30°，
在直角△BPE中，BE=$\frac{\sqrt{3}}{3}$PE=$\frac{\sqrt{3}}{3}$x米，
∵AB=AE-BE=9米，
则x-$\frac{\sqrt{3}}{3}$x=9，
解得：x=$\frac{27+9\sqrt{3}}{2}$．
则BE=$\frac{9\sqrt{3}+9}{2}$米．
在直角△BEQ中，QE=$\frac{\sqrt{3}}{3}$BE=$\frac{9+3\sqrt{3}}{2}$米．
∴PQ=PE-QE=$\frac{27+9\sqrt{3}}{2}$-$\frac{9+3\sqrt{3}}{2}$=9+3$\sqrt{3}$（米）．
答：电线杆PQ的高度为（9+3$\sqrt{3}$）米．

点评 本题考查了仰角的定义、解直角三角形、三角函数；运用三角函数求出PE和QE是解决问题的关键．