
分析 (1)设乙的平均速度为x米/秒,根据,甲运动50m与乙运动(50-4)m所用时间相等,可得方程,解出即可.
(2)不能同时到达,设调整后乙的平均速度为y,根据时间相等,得出方程求解即可.
解答 解:(1)设乙的平均速度为x米/秒,
由题意得,
$\frac{50}{2.5}=\frac{50-4}{x}$,
解得:x=2.2,
经检验x=2.2是原方程的解.
答:甲的平均速度2.2m/s.
(2)不能同时到达.
设调整后乙的平均速度为ym/s,
$\frac{54}{2.5}=\frac{50}{y}$,
解得:y≈2.3.
答:调整乙的车速为2.3m/s可使两车能同时到达终点.
点评 本题考查了分式方程的应用,解答本题的关键是仔细审题,找到等量关系,建立方程,难度一般.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
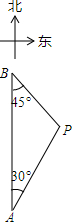 如图,A、B两座城市相距100千米,现计划在两城市间修筑一条高速公路(即线段AB).经测量,森林保护区中心P点既在A城市的北偏东30°的方向上,又在B城市的南偏东45°的方向上.已知森林保护区的范围是以P为圆心,35千米为半径的圆形区域内.请问:计划修筑的这条高速公路会不会穿越森林保护区?请通过计算说明.(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
如图,A、B两座城市相距100千米,现计划在两城市间修筑一条高速公路(即线段AB).经测量,森林保护区中心P点既在A城市的北偏东30°的方向上,又在B城市的南偏东45°的方向上.已知森林保护区的范围是以P为圆心,35千米为半径的圆形区域内.请问:计划修筑的这条高速公路会不会穿越森林保护区?请通过计算说明.(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=x2+1 | B. | y=x2-1 | C. | y=(x+1)2 | D. | y=(x-1)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知线段AB,点C在线段AB上,AC=4,BC=6,点M、N分别是线段AC、BC的中点.
如图,已知线段AB,点C在线段AB上,AC=4,BC=6,点M、N分别是线段AC、BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③④ | B. | ①③⑤⑦ | C. | ②③④⑥ | D. | ②④⑤⑦ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走9m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走9m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com