
科目:初中数学 来源: 题型:
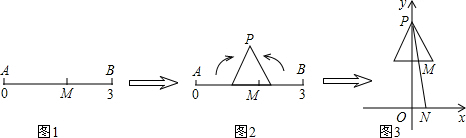
 如图,将连续的奇数1、3、5、7 …,排列成如下的数表,用十字框框出5个数.问:
如图,将连续的奇数1、3、5、7 …,排列成如下的数表,用十字框框出5个数.问:查看答案和解析>>
科目:初中数学 来源: 题型:
| A、1.5×107万吨 |
| B、1.5×103万吨 |
| C、15×102万吨 |
| D、0.15×104万吨 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| AM |
| DN |
查看答案和解析>>
科目:初中数学 来源: 题型:
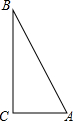 如图,△ABC是直角三角形,∠ACB=90°,在△ABC内剪出一块半圆,使圆心在BC边上,且半圆的弧与边AB相切.
如图,△ABC是直角三角形,∠ACB=90°,在△ABC内剪出一块半圆,使圆心在BC边上,且半圆的弧与边AB相切.查看答案和解析>>
科目:初中数学 来源: 题型:
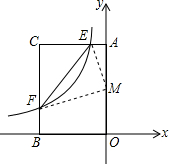 如图,在平面直角坐标系xOy中,矩形AOBC的AO边在y轴上,BO边在x轴上,C点坐标为(-2,3),反比例函数y=
如图,在平面直角坐标系xOy中,矩形AOBC的AO边在y轴上,BO边在x轴上,C点坐标为(-2,3),反比例函数y=| k |
| x |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
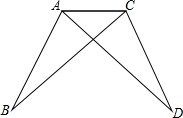 如图,小明在完成数学作业时,遇到了这样一个问题,AB=CD,AD=BC,请说明∠B=∠D的道理,小明动手测量了一下,发现∠B确实与∠D相等,但他不能说明其中的道理,你能帮助他说明这个道理吗?试试看.
如图,小明在完成数学作业时,遇到了这样一个问题,AB=CD,AD=BC,请说明∠B=∠D的道理,小明动手测量了一下,发现∠B确实与∠D相等,但他不能说明其中的道理,你能帮助他说明这个道理吗?试试看.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com