
【题目】某企业生产并销售某种产品,整理出该商品在第![]() (
(![]() )天的售价
)天的售价![]() 与
与![]() 函数关系如图所示,已知该商品的进价为每件30元,第
函数关系如图所示,已知该商品的进价为每件30元,第![]() 天的销售量为
天的销售量为![]() 件.
件.
(1)试求出售价![]() 与
与![]() 之间的函数关系是;
之间的函数关系是;
(2)请求出该商品在销售过程中的最大利润;
(3)在该商品销售过程中,试求出利润不低于3600元的![]() 的取值范围.
的取值范围.

【答案】(1)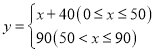 ;(2)6050;(3)
;(2)6050;(3)![]() .
.
【解析】
(1)当1≤x≤50时,设商品的售价y与时间x的函数关系式为y=kx+b,由点的坐标利用待定系数法即可求出此时y关于x的函数关系式,根据图形可得出当50≤x≤90时,y=90;
(2)根据W关于x的函数关系式,分段考虑其最值问题.当1≤x≤50时,结合二次函数的性质即可求出在此范围内W的最大值;当50≤x≤90时,根据一次函数的性质即可求出在此范围内W的最大值,两个最大值作比较即可得出结论;
(3)分当![]() 时与当
时与当![]() 时利用二次函数与一次函数的性质进行得到
时利用二次函数与一次函数的性质进行得到![]() 的取值范围.
的取值范围.
(1)当![]() 时,
时,
设![]() .
.
∵图象过(0,40),(50,90),
∴![]() 解得
解得![]() ,
,
∴![]() ,
,
∴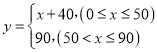
(2)当![]() 时,
时,
![]()
![]()
∵![]() ,
,
∴当![]() 时,
时,![]() 元;
元;
当![]() 时,
时,
![]()
∵![]() ,
,
∴当![]() 时,
时,![]() 元.
元.
∵![]() ,
,
∴当![]() 时,
时,![]() 元
元
(3)当![]() 时,
时,![]()
令![]() ,解得:
,解得:![]() ,
,![]() ,
,
∵![]()
∴当![]() 时,利润不低于3600元;
时,利润不低于3600元;
当![]() 时,
时,![]()
∵![]() ,即
,即![]() ,
,
解得![]() ,
,
∴此时![]() ;
;
综上,当![]() 时,利润不低于3600元.
时,利润不低于3600元.


科目:初中数学 来源: 题型:
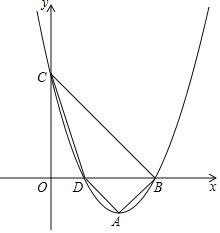
【题目】如图,已知二次函数y=x2﹣4x+3图象与x轴分别交于点B、D,与y轴交于点C,顶点为A,分别连接AB,BC,CD,DA.
(1)求四边形ABCD的面积;
(2)当y>0时,自变量x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
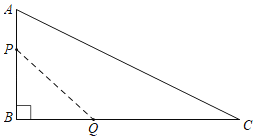
【题目】如图所示,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始,以2mm/S的速度沿边AB向B移动(不与点B重合),动点Q从点B开始,以4m/s的速度沿边BC向C移动(不与C重合),如果P、Q分别从A、B同时出发,设运动的时间为xs,四边形APQC的面积为ymm2.
(1)写出y与x之间的函数表达式;
(2)当x=2时,求四边形APQC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小华同学设计的“作三角形的高线”的尺规作图的过程.
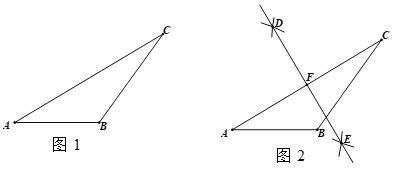
已知:如图1,△ABC.
求作:AB边上的高线.
作法:如图2,
①分别以A,C为圆心,大于![]() 长
长
为半径作弧,两弧分别交于点D,E;
② 作直线DE,交AC于点F;
③ 以点F为圆心,FA长为半径作圆,交AB的延长线于点M;
④ 连接CM.
则CM 为所求AB边上的高线.
根据上述作图过程,回答问题:
(1)用直尺和圆规,补全图2中的图形;
(2)完成下面的证明:
证明:连接DA,DC,EA,EC,
∵由作图可知DA=DC =EA=EC,
∴DE是线段AC的垂直平分线.
∴FA=FC .
∴AC是⊙F的直径.
∴∠AMC=______°(___________________________________)(填依据),
∴CM⊥AB.
即CM就是AB边上的高线.
查看答案和解析>>
科目:初中数学 来源: 题型:
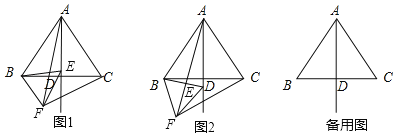
【题目】已知△ABC是等边三角形,AD⊥BC于点D,点E是直线AD上的动点,将BE绕点B顺时针方向旋转60°得到BF,连接EF、CF、AF.
(1)如图1,当点E在线段AD上时,猜想∠AFC和∠FAC的数量关系;(直接写出结果)
(2)如图2,当点E在线段AD的延长线上时,(1)中的结论还成立吗?若成立,请证明你的结论,若不成立,请写出你的结论,并证明你的结论;
(3)点E在直线AD上运动,当△ACF是等腰直角三角形时,请直接写出∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真阅读下面的数学小探究,完成所提出的问题
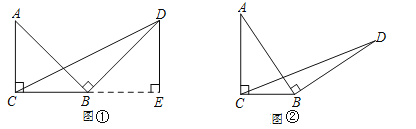
(1)探究1,如图①,在等腰直角三角形ABC中,∠ACB=90°,BC=3,将边 AB绕点B顺时针旋转90°得到线段BD,连接CD,过点D作BC边上的高DE,则DE与BC的数量关系是 . △BCD的面积为 .
(2)探究2,如图②,在一般的Rt△ABC中,∠ACB=90°,BC=![]() ,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,请用含
,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,请用含![]() 的式子表示△BCD的面积,并说明理由.
的式子表示△BCD的面积,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
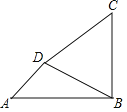
【题目】如图,海中有两个小岛![]() ,
,![]() ,某渔船在海中的
,某渔船在海中的![]() 处测得小岛D位于东北方向上,且相距
处测得小岛D位于东北方向上,且相距![]() ,该渔船自西向东航行一段时间到达点
,该渔船自西向东航行一段时间到达点![]() 处,此时测得小岛
处,此时测得小岛![]() 恰好在点
恰好在点![]() 的正北方向上,且相距
的正北方向上,且相距![]() ,又测得点
,又测得点![]() 与小岛
与小岛![]() 相距
相距![]() .
.
(1)求![]() 的值;
的值;
(2)求小岛![]() ,
,![]() 之间的距离(计算过程中的数据不取近似值).
之间的距离(计算过程中的数据不取近似值).
查看答案和解析>>
科目:初中数学 来源: 题型:
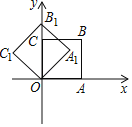
【题目】如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2018次得到正方形OA2018B2018C2018,如果点A的坐标为(1,0),那么点B2018的坐标为( )
A. (1,1) B. (0,![]() ) C. (
) C. (![]() ) D. (﹣1,1)
) D. (﹣1,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两块全等的直角三角形如图1摆放在一起,设较短直角边为1.现将Rt△BCD沿射线BD方向平移到Rt△B1C1D1的位置(如图2).
(1)求证:四边形ABC1D1是平行四边形;
(2)当四边形ABC1D1为矩形时,求矩形ABC1D1的面积;
(3)当点B的移动距离为多少时,四边形ABC1D1为菱形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com