
ΓΨΧβΡΩΓΩ»γΆΦΥυ ΨΘ§‘ΎΓςABC÷–Θ§ΓœBΘΫ90ΓψΘ§ABΘΫ12mmΘ§BCΘΫ24mmΘ§Ε·ΒψP¥”ΒψAΩΣ ΦΘ§“‘2mm/SΒΡΥΌΕ»―Ί±ΏABœρB“ΤΕ·Θ®≤Μ”κΒψB÷ΊΚœΘ©Θ§Ε·ΒψQ¥”ΒψBΩΣ ΦΘ§“‘4m/sΒΡΥΌΕ»―Ί±ΏBCœρC“ΤΕ·Θ®≤Μ”κC÷ΊΚœΘ©Θ§»γΙϊPΓΔQΖ÷±π¥”AΓΔBΆ§ ±≥ωΖΔΘ§…η‘ΥΕ·ΒΡ ±ΦδΈΣxsΘ§ΥΡ±Ώ–ΈAPQCΒΡΟφΜΐΈΣymm2Θ°
Θ®1Θ©–¥≥ωy”κx÷°ΦδΒΡΚ· ΐ±μ¥ο ΫΘΜ
Θ®2Θ©Β±xΘΫ2 ±Θ§«σΥΡ±Ώ–ΈAPQCΒΡΟφΜΐΘ°
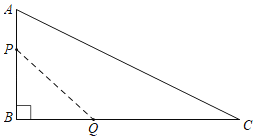
ΓΨ¥πΑΗΓΩΘ®1Θ©yΘΫ4x2©¹24x+144ΘΜΘ®2Θ©112mm2Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©”Οx±μ ΨPBΚΆBQΘ°άϊ”ΟΝΫΗω÷±Ϋ«»ΐΫ«–ΈΒΡΟφΜΐ≤ν«σΒΟ¥πΑΗΦ¥Ω…ΘΜ
Θ®2Θ©«σ≥ωxΘΫ2 ±Θ§yΒΡ÷ΒΦ¥Ω…ΒΟΘ°
ΫβΘΚΘ®1Θ©ΓΏ‘ΥΕ· ±ΦδΈΣxΘ§ΒψPΒΡΥΌΕ»ΈΣ2mm/sΘ§ΒψQΒΡΥΌΕ»ΈΣ4mm/sΘ§
ΓύPBΘΫ12©¹2xΘ§BQΘΫ4xΘ§
ΓύyΘΫ![]() Θ°
Θ°
Θ®2Θ©Β±xΘΫ2 ±Θ§yΘΫ4ΓΝ22©¹24ΓΝ2+144ΘΫ112Θ§
Φ¥Β±xΘΫ2 ±Θ§ΥΡ±Ώ–ΈAPQCΒΡΟφΜΐΈΣ112mm2Θ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
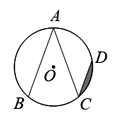
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΒψAΘ§BΘ§CΘ§D‘ΎΓ―O…œΘ§AB=ACΘ§ΓœA=40ΓψΘ§CDΓΈABΘ§»τΓ―OΒΡΑκΨΕΈΣ2Θ§‘ρΆΦ÷–“θ”Α≤ΩΖ÷ΒΡΟφΜΐ «(ΓΓΓΓ)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥…Χ≥Γ“ΣΨ≠”Σ“Μ÷÷–¬…œ –ΒΡΈΡΨΏΘ§ΫχΦέΈΣ20‘ΣΘ§ ‘”ΣœζΫΉΕΈΖΔœ÷ΘΚΒ±œζ έΒΞΦέ «25‘Σ ±Θ§ΟΩΧλΒΡœζ έΝΩΈΣ250ΦΰΘ§œζ έΒΞΦέΟΩ…œ’«1‘ΣΘ§ΟΩΧλΒΡœζ έΝΩΨΆΦθ…Ό10Φΰ
Θ®1Θ©–¥≥ω…Χ≥Γœζ έ’β÷÷ΈΡΨΏΘ§ΟΩΧλΥυΒΟΒΡœζ έάϊ»σ![]() Θ®‘ΣΘ©”κœζ έΒΞΦέ
Θ®‘ΣΘ©”κœζ έΒΞΦέ![]() Θ®‘ΣΘ©÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ
Θ®‘ΣΘ©÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ
Θ®2Θ©«σœζ έΒΞΦέΈΣΕύ…Ό‘Σ ±Θ§ΗΟΈΡΨΏΟΩΧλΒΡœζ έάϊ»σΉν¥σΘΜ
Θ®3Θ©…Χ≥ΓΒΡ”Σœζ≤ΩΫαΚœ…œ ω«ιΩωΘ§Χα≥ωΝΥAΓΔBΝΫ÷÷”ΣœζΖΫΑΗ
ΖΫΑΗAΘΚΗΟΈΡΨΏΒΡœζ έΒΞΦέΗΏ”ΎΫχΦέ«“≤Μ≥§Ιΐ30‘ΣΘΜ
ΖΫΑΗBΘΚΟΩΧλœζ έΝΩ≤Μ…Ό”Ύ10ΦΰΘ§«“ΟΩΦΰΈΡΨΏΒΡάϊ»σ÷Ν…ΌΈΣ25‘Σ
«κ±»ΫœΡΡ÷÷ΖΫΑΗΒΡΉν¥σάϊ»σΗϋΗΏΘ§≤ΔΥΒΟςάμ”…
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣ”Σ‘λΓΑΑ≤»Ϊ≥ω––Γ±ΒΡΝΦΚΟΫΜΆ®Ζ’Έß, Β ±ΦύΩΊΒά¬ΖΫΜ±≈,Ρ≥ –ΫΜΙή≤ΩΟ≈‘Ύ¬ΖΩΎΑ≤ΉΑΒΡΗΏ«ε…ψœώΆΖ»γΆΦΥυ Ψ,ΝΔΗΥMA”κΒΊΟφAB¥Ι÷±,–±ά≠ΗΥCD”κAMΫΜ”ΎΒψC,ΚαΗΥDEΓΈAB,…ψœώΆΖEFΓΆDE”ΎΒψE,AC=55ΟΉ,CD=3ΟΉ,EF=0.4ΟΉ,ΓœCDE=162ΓψΓΘ
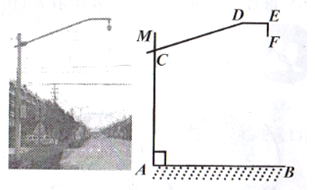
Θ®1Θ©«σΓœMCDΒΡΕ» ΐΘΜ
Θ®2Θ©«σ…ψœώΆΖœ¬ΕΥΒψFΒΫΒΊΟφABΒΡΨύάκΓΘ(ΨΪ»ΖΒΫΑΌΖ÷ΈΜ)
Θ®≤ΈΩΦ ΐΨί;sin72Γψ=0.95Θ§cos72ΓψΓ÷0.31,tan72Γψ=3.08,sin18ΓψΓ÷0.31,cos18ΓψΓ÷0.95,tan18ΓψΓ÷0.32Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
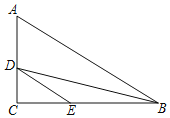
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΓςABC÷–Θ§ΓœCΘΫ90ΓψΘ§ΓœBΘΫ30ΓψΘ§ACΘΫ![]() Θ§DΓΔEΖ÷±π‘Ύ±ΏACΓΔBC…œΘ§CDΘΫ1Θ§DEΓΈABΘ§ΫΪΓςCDE»ΤΒψC–ΐΉΣΘ§–ΐΉΣΚσΒψDΓΔEΕ‘”ΠΒΡΒψΖ÷±πΈΣDΓδΓΔEΓδΘ§Β±ΒψEΓδ¬δ‘ΎœΏΕΈADΓδ…œ ±Θ§Ν§Ϋ”BEΓδΘ§¥Υ ±BEΓδΒΡ≥ΛΈΣΘ®ΓΓΓΓΘ©
Θ§DΓΔEΖ÷±π‘Ύ±ΏACΓΔBC…œΘ§CDΘΫ1Θ§DEΓΈABΘ§ΫΪΓςCDE»ΤΒψC–ΐΉΣΘ§–ΐΉΣΚσΒψDΓΔEΕ‘”ΠΒΡΒψΖ÷±πΈΣDΓδΓΔEΓδΘ§Β±ΒψEΓδ¬δ‘ΎœΏΕΈADΓδ…œ ±Θ§Ν§Ϋ”BEΓδΘ§¥Υ ±BEΓδΒΡ≥ΛΈΣΘ®ΓΓΓΓΘ©
A.2![]() B.3
B.3![]() C.2
C.2![]() D.3
D.3![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
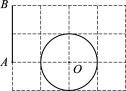
ΓΨΧβΡΩΓΩ»γΆΦΥυ ΨΒΡΆχΗώ «’ΐΖΫ–ΈΆχΗώΘ§œΏΕΈAB»ΤΒψAΥ≥ ±’κ–ΐΉΣΠΝΘ®0ΓψΘΦΠΝΘΦ180ΓψΘ©Κσ”κΓ―Oœύ«–Θ§‘ρΠΝΒΡ÷ΒΈΣ_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
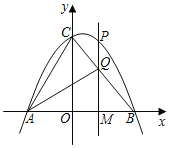
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏyΘΫ©¹![]() x2+bx+cΫΜx÷α”ΎAΘ®©¹3Θ§0Θ©Θ§BΘ®4Θ§0Θ©ΝΫΒψΘ§”κy÷αΫΜ”ΎΒψCΘ§Ν§Ϋ”ACΘ§BCΘ°
x2+bx+cΫΜx÷α”ΎAΘ®©¹3Θ§0Θ©Θ§BΘ®4Θ§0Θ©ΝΫΒψΘ§”κy÷αΫΜ”ΎΒψCΘ§Ν§Ϋ”ACΘ§BCΘ°
Θ®1Θ©«σ¥Υ≈ΉΈοœΏΒΡ±μ¥ο ΫΘΜ
Θ®2Θ©«σΙΐBΓΔCΝΫΒψΒΡ÷±œΏΒΡΚ· ΐ±μ¥ο ΫΘΜ
Θ®3Θ©ΒψP «ΒΎ“ΜœσœόΡΎ≈ΉΈοœΏ…œΒΡ“ΜΗωΕ·ΒψΘ°ΙΐΒψPΉςPMΓΆx÷αΘ§¥ΙΉψΈΣΒψMΘ§PMΫΜBC”ΎΒψQΘ° ‘ΧΫΨΩΒψP‘Ύ‘ΥΕ·Ιΐ≥Χ÷–Θ§ «Ζώ¥φ‘Ύ’β―υΒΡΒψQΘ§ ΙΒΟ“‘AΘ§CΘ§QΈΣΕΞΒψΒΡ»ΐΫ«–Έ «Β»―ϋ»ΐΫ«–ΈΘ°»τ¥φ‘ΎΘ§«κ«σ≥ω¥Υ ±ΒψPΒΡΉχ±ξΘ§»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…ΘΜ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥Τσ“Β…ζ≤ζ≤Δœζ έΡ≥÷÷≤ζΤΖΘ§’ϊάμ≥ωΗΟ…ΧΤΖ‘ΎΒΎ![]() (
(![]() )ΧλΒΡ έΦέ
)ΧλΒΡ έΦέ![]() ”κ
”κ![]() Κ· ΐΙΊœΒ»γΆΦΥυ ΨΘ§“―÷ΣΗΟ…ΧΤΖΒΡΫχΦέΈΣΟΩΦΰ30‘ΣΘ§ΒΎ
Κ· ΐΙΊœΒ»γΆΦΥυ ΨΘ§“―÷ΣΗΟ…ΧΤΖΒΡΫχΦέΈΣΟΩΦΰ30‘ΣΘ§ΒΎ![]() ΧλΒΡœζ έΝΩΈΣ
ΧλΒΡœζ έΝΩΈΣ![]() ΦΰΘ°
ΦΰΘ°
Θ®1Θ© ‘«σ≥ω έΦέ![]() ”κ
”κ![]() ÷°ΦδΒΡΚ· ΐΙΊœΒ «ΘΜ
÷°ΦδΒΡΚ· ΐΙΊœΒ «ΘΜ
Θ®2Θ©«κ«σ≥ωΗΟ…ΧΤΖ‘Ύœζ έΙΐ≥Χ÷–ΒΡΉν¥σάϊ»σΘΜ
Θ®3Θ©‘ΎΗΟ…ΧΤΖœζ έΙΐ≥Χ÷–Θ§ ‘«σ≥ωάϊ»σ≤ΜΒΆ”Ύ3600‘ΣΒΡ![]() ΒΡ»Γ÷ΒΖΕΈßΘ°
ΒΡ»Γ÷ΒΖΕΈßΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
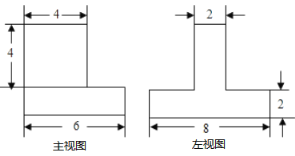
ΓΨΧβΡΩΓΩ»γΆΦΘ§ «”…ΝΫΗω≥ΛΖΫΧεΉιΚœΕχ≥…ΒΡ“ΜΗωΝΔΧεΆΦ–ΈΒΡ÷ς ”ΆΦΚΆΉσ ”ΆΦΘ§ΗυΨίΆΦ÷–Υυ±ξ≥Ώ¥γ(ΒΞΈΜ: ![]() )Θ°
)Θ°
(1)÷±Ϋ”–¥≥ω…œœ¬ΝΫΗω≥ΛΖΫ–ίΒΡ≥ΛΓΔΩμΓΔ…ΧΖ÷±π «Εύ…Ό:
(2)«σ’βΗωΝΔΧεΆΦ–ΈΒΡΧεΜΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com