
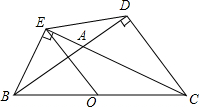
 如图,△BCD和△BCE中,∠BDC=∠BEC=90°,O为BC的中点,BD,CE交于A,∠BAC=120°,求证:DE=OE.
如图,△BCD和△BCE中,∠BDC=∠BEC=90°,O为BC的中点,BD,CE交于A,∠BAC=120°,求证:DE=OE. 分析 连接OD,根据直角三角形斜边上的中线等于斜边的一半可得OD=OE=OB=OC,根据等边对等角可得∠CBA=∠BDO,∠BCA=∠CEO,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BOE=2∠BCA,∠COD=2∠CBA,再根据三角形的内角和等于180°求出∠CBA+∠BCA=60°,然后求出∠DOE=60°,从而判断出△DOE是等边三角形,最后根据等边三角形的三条边都相等证明即可.
解答 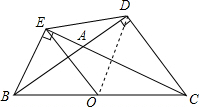 证明:如图,连接OD,
证明:如图,连接OD,
∵∠BDC=∠BEC=90°,O为BC的中点,
∴OD=OE=OB=OC,
∴∠CBA=∠BDO,∠BCA=∠CEO,
由三角形的外角性质得,∠BOE=∠BCA+∠CEO=2∠BCA,
∠COD=∠CBA+∠BDO=2∠CBA,
∵∠BAC=120°,
∴∠CBA+∠BCA=180°-120°=60°,
∴∠DOE=60°,
∴△DOE是等边三角形,
∴DE=OE.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等边三角形的判定与性质,三角形的一个外角等于与它不相邻的两个内角的和的性质以及三角形的内角和定理,难点在于求出等边三角形.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:选择题
| A. | 对任意实数k,函数与x轴都没有交点 | |
| B. | 存在实数n,满足当x≥n时,函数y的值都随x的增大而减小 | |
| C. | k取不同的值时,二次函数y的顶点始终在同一条直线上 | |
| D. | 对任意实数k,抛物线y=x2+2kx+k-1都必定经过唯一定点 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
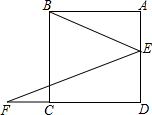 如图,点E为正方形ABCD的边AD上一点,F在DC的延长线上,且CF=AE.
如图,点E为正方形ABCD的边AD上一点,F在DC的延长线上,且CF=AE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
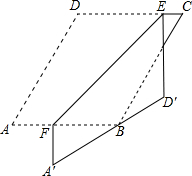 如图,在?ABCD纸片中,∠A=60°,AD-AB=1,点E,F分别在边CD,AB上,将纸片沿EF折叠,使点A,D分别落在点A′,D′,处,且AD经过点B.当D′E⊥CD时,CE=1,则AB的长是$\frac{3\sqrt{3}+5}{2}$.
如图,在?ABCD纸片中,∠A=60°,AD-AB=1,点E,F分别在边CD,AB上,将纸片沿EF折叠,使点A,D分别落在点A′,D′,处,且AD经过点B.当D′E⊥CD时,CE=1,则AB的长是$\frac{3\sqrt{3}+5}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
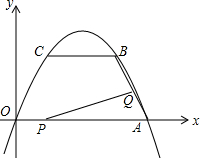 已知抛物线y=ax2+bx+c经过O(0,0),A(4,0),B(3,$\sqrt{3}$)三点,连结AB,过点B作BC∥x轴交该抛物线于点C.
已知抛物线y=ax2+bx+c经过O(0,0),A(4,0),B(3,$\sqrt{3}$)三点,连结AB,过点B作BC∥x轴交该抛物线于点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
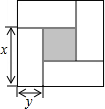 如图是用4个相同的小矩形与1个小正方形密铺而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y(其中x>y)表示小矩形的长与宽,请观察图案,指出以下关系式中不正确的是( )
如图是用4个相同的小矩形与1个小正方形密铺而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y(其中x>y)表示小矩形的长与宽,请观察图案,指出以下关系式中不正确的是( )| A. | x+y=7 | B. | x-y=2 | C. | x2-y2=4 | D. | 4xy+4=49 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com