
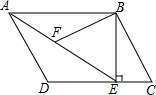
 如图,在平行四边形ABCD中,过B作BE⊥CD,垂足为点E,连接AE,F为AE上一点,且∠BFE=∠C.
如图,在平行四边形ABCD中,过B作BE⊥CD,垂足为点E,连接AE,F为AE上一点,且∠BFE=∠C.8
| ||
| 3 |


科目:初中数学 来源: 题型:
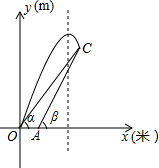 如图是某次军事演习迫击炮射击目标时在平面直角坐标系中的示意图,地面有O、A两个观测点,分别测得目标C的仰角为α、β,OA=20米,tanα=
如图是某次军事演习迫击炮射击目标时在平面直角坐标系中的示意图,地面有O、A两个观测点,分别测得目标C的仰角为α、β,OA=20米,tanα=| 3 |
| 2 |
| 9 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、一个数的相反数不是负数,这个数一定是负数 |
| B、一个数的绝对值是正数,这个数一定是正数 |
| C、两个数的和是正数,这两个数一定都是正数 |
| D、两个数的乘积为1,这两个数一定互为倒数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com