
【题目】如图,![]() 的平分线过点
的平分线过点![]() ,以
,以![]() 点为圆心的圆与
点为圆心的圆与![]() 相切于点
相切于点![]() ,
,![]() 为
为![]() 的直径.
的直径.
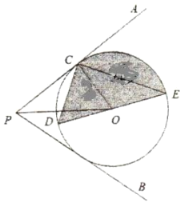
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() ;
;
(3)若![]() 的半径为
的半径为![]() ,
,![]() ,求阴影部分的面积.
,求阴影部分的面积.
【答案】(1)证明见解析,(2)![]() (3)
(3)![]()
【解析】
(1)过点O作OH⊥PB,证明OH=OC即可;
(2)由圆周角定理求出∠COD=2∠E=50°,由切线求出∠COP的度数,∠COD-∠COP即可得到答案;
(3)在Rt△CDE中,由三角函数先求出∠E的度数为30°,进而求出圆心角∠COE=120°,再由扇形面积公式算出扇形COE的面积,再加上等边△CDO的面积及得到阴影部分的面积.
解:(1)证明:过点O作OH⊥PB于H点,如下图所示:
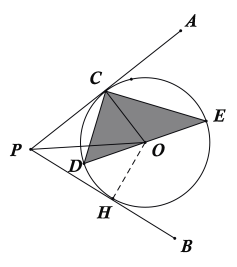
∵AP为圆O的切线,且C为切点
∴CO⊥PC
∵PO为∠APB的角平分线,且CO⊥PC,OH⊥PB
∴OH=OC
故PB是圆O的切线.
(2)∵∠CPO=50°,且CP⊥CO
∴∠COP=90°-50°=40°
又由同弧所对的圆周角是圆心角的一半可知
∠COD=2∠E=2×25°=50°
∴∠POD=∠COD-∠COP=50°-40°=10°.
故答案为:10°.
(3)∵DE为圆O的直径
∴在Rt△DEC中,![]()
∴∠E=30°
∴∠COE=180°-30°-30°=120°
∴扇形COE的面积为:![]()
∴△CDO的面积为:![]()
故阴影部分的面积为:![]()
故答案为:![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】英语老师对某班级全班同学进行口语测试,并按10分制评分,将评分结果制成了如图两幅统计图(不完整).请根据图表信息,解答下列问题:
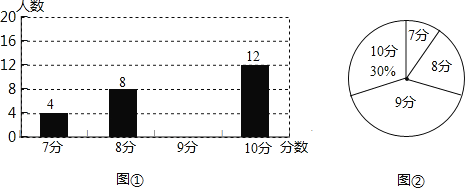
(1)求该班级学生总人数,并将条形统计图补充完整;
(2)求该班学生口语测试所得分数的平均分;
(3)英语老师将随机邀请该班一名同学进行口语对话,求事件“英语老师邀请得分为9分的同学进行口语对话”发生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
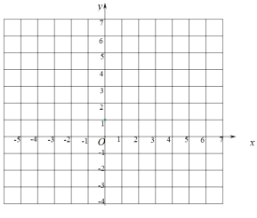
(1)根据给定的条件,则![]() _________,
_________,![]() ____________.
____________.
(2)在给出的平面直角坐标系中,画出函数图像;
(3)①结合所画的图像,直接写出方程![]() 的解,解为________________.(精确到十分位)
的解,解为________________.(精确到十分位)
②若一次函数![]() 的图像与
的图像与![]() 的图像有且只有三个交点,则
的图像有且只有三个交点,则![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,tan∠BACtan∠ABC=1,⊙O经过A、B两点,分别交AC、BC于D、E两点,若DE=10,AB=24,则⊙O的半径为____.
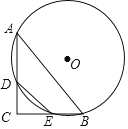
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校某数学兴趣小组想测学校旗杆高度如图,明明在稻香园一楼![]() 点测得旗杆顶点
点测得旗杆顶点![]() 仰角为
仰角为![]() ,在稻香园二楼
,在稻香园二楼![]() 点测得点
点测得点![]() 的仰角为
的仰角为![]() .明明从
.明明从![]() 点朝旗杆方向步行
点朝旗杆方向步行![]() 米到
米到![]() 点,沿坡度
点,沿坡度![]() 的台阶走到点
的台阶走到点![]() ,再向前走
,再向前走![]() 米到旗杆底部
米到旗杆底部![]() ,已知稻香园
,已知稻香园![]() 高度为
高度为![]() 米,则旗杆
米,则旗杆![]() 的高度约为( )(参考数据:
的高度约为( )(参考数据:![]() ,
,![]() ,
,![]() )
)
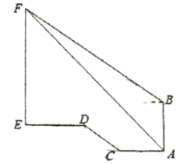
A.![]() 米B.
米B.![]() 米C.
米C.![]() 米D.
米D.![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC与△ABD中,∠DBA=∠CAB,AC与BD交于点F
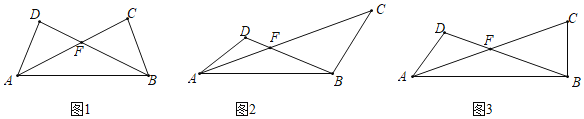
(1)如图1,若∠DAF=∠CBF,求证:AD=BC;
(2)如图2,∠D=135°,∠C=45°,AD=2,AC=4,求BD的长.
(3)如图3,若∠DBA=18°,∠D=108°,∠C=72°,AD=1,直接写出DB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过点A(-3,0),C(0,3),交x轴于另一点B,其顶点为D.
经过点A(-3,0),C(0,3),交x轴于另一点B,其顶点为D.
(1)求抛物线的解析式;
(2)点P为抛物线上一点,直线CP交x轴于点E,若△CAE与△OCD相似,求P点坐标;
(3)如果点F在y轴上,点M在直线AC上,那么在抛物线上是否存在点N,使得以C,F,M,N为顶点的四边形是菱形?若存在,请求出菱形的周长;若不存在,请说明理由.
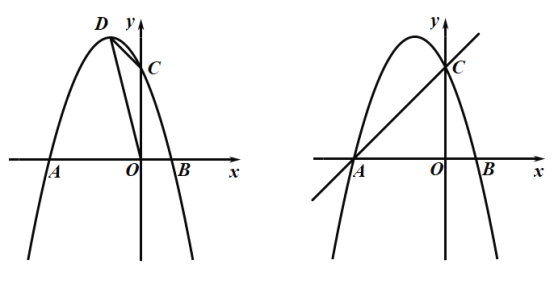
查看答案和解析>>
科目:初中数学 来源: 题型:
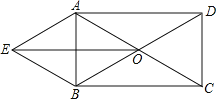
【题目】如图,矩形ABCD中,对角线AC,BD交于点O,以AD,OD为邻边作平行四边形ADOE,连接BE.
(1)求证:四边形AOBE是菱形;
(2)若∠EAO+∠DCO=180°,DC=3,求四边形ADOE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com