
| A、2 | B、1 | C、0 | D、3 |


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
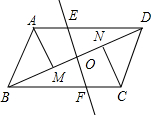 如图,?ABCD中,O是对角线BD中点,过点O的直线和AD、BC分别相交于E、F,AM平分∠BAD,CN平分∠DCB.请在平行四边形ABCD的基础上添加适当的条件,构造新的平行四边形,进而谈谈你的感想.
如图,?ABCD中,O是对角线BD中点,过点O的直线和AD、BC分别相交于E、F,AM平分∠BAD,CN平分∠DCB.请在平行四边形ABCD的基础上添加适当的条件,构造新的平行四边形,进而谈谈你的感想.查看答案和解析>>
科目:初中数学 来源: 题型:
| b-1 |
| a-1 |
| a-1 |
| b-1 |
| A、-20 | B、2 |
| C、2或-20 | D、2或20 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,矩形ABCD中,AB=6cm,AC=10cm,有一动点P,从点B开始,沿由B向A,再由A向D,再由D向C的方向运动,已知每秒钟点P的运动方向距离为2cm,试求△PBC的面积S(cm2)与运动时间t(秒)的函数关系式,并写出自变量t的取值范围.
如图,矩形ABCD中,AB=6cm,AC=10cm,有一动点P,从点B开始,沿由B向A,再由A向D,再由D向C的方向运动,已知每秒钟点P的运动方向距离为2cm,试求△PBC的面积S(cm2)与运动时间t(秒)的函数关系式,并写出自变量t的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:
| 甲种原料x克 | 乙种原料y克 | 所配置的营养品 | |
| 所含蛋白质(单位) | 0.5x | ||
| 所含铁质(单位) | 0.4y |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com