
【题目】如图,Rt△ACB中,∠ACB=90°,O为AB的中点,AE=AO,BF=BO,OE=2![]() ,OF=3,则AB的长为( )
,OF=3,则AB的长为( )
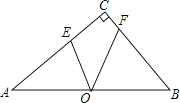
A.![]() B.5C.8D.
B.5C.8D.![]()
【答案】A
【解析】
延长FO至H,使OH=OF,连接AH,EH,利用全等三角形的判定和性质可证得BF=AH=AE=AO=OB,再利用勾股定理解答即可.
解:延长FO至H,使OH=OF,连接AH,EH,
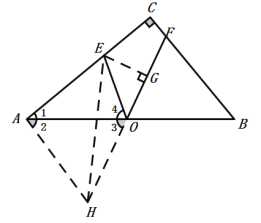
∵AO=OB,OH=OF,∠AOH=∠BOF,
在△AOH与△BOF中,
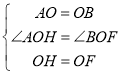 ,
,
∴△AOH≌△BOF(SAS),
∴BF=AH=AE=AO=OB,
∴∠2=∠B,
∴∠1+∠B=∠1+∠2=90![]() ,
,
∠3=∠AHO=![]() ,
,
∠4=∠AEO=![]() ,
,
∴∠3+∠4=![]()
=180![]() -
-![]() =135
=135![]() ,
,
过E作EG⊥FH,在Rt△EOG中,∠EOG=45![]() ,EO=2
,EO=2![]() ,
,
∴OG=EG=2,
∴HG=3+2=5,
∴![]() ,
,
在Rt△EAH中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
故选:A.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,四边形![]() 是矩形,点
是矩形,点![]() ,点
,点![]() ,点
,点![]() .以
.以![]() 点为中心,顺时针旋转矩形
点为中心,顺时针旋转矩形![]() ,得到矩形
,得到矩形![]() ,点
,点![]() 的对应点分别为
的对应点分别为![]() ,记旋转角为
,记旋转角为![]() .
.
(1)如图①,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
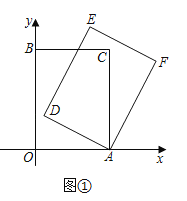
(2)如图②,当点![]() 落在
落在![]() 的延长线上时,求点
的延长线上时,求点![]() 的坐标;
的坐标;

(3)当点![]() 落在线段
落在线段![]() 上时,求点
上时,求点![]() 的坐标(直接写出结果即可).
的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为每件![]() 元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于
元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于![]() ,经试销发现,销售量
,经试销发现,销售量![]() (件)与销售单价
(件)与销售单价![]() (元)的关系符合一次函数
(元)的关系符合一次函数![]() .
.
![]() 直接写出销售单价
直接写出销售单价![]() 的取值范围,
的取值范围,
![]() 若销售该服装获得利润为
若销售该服装获得利润为![]() 元,试写出利润
元,试写出利润![]() 与销售单价
与销售单价![]() 之间的关系式;销售单价为多少元时,可获得最大利润,最大利润是多少元?
之间的关系式;销售单价为多少元时,可获得最大利润,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,其中正确的有( )
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,其中正确的有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯.如图所示,已知原阶梯式扶梯AB长为10m,坡角∠ABD=30°;改造后斜坡式自动扶梯的坡角∠ACB=9°,请计算改造后的斜坡AC的长度,(结果精确到0.01(sin9°≈0.156,cos9°≈0.988,tan9°≈0.158)
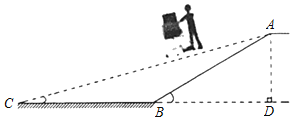
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】武汉市政府大力扶持大学生创业,童威在政府的扶持下投资销售一种进价为每盏20元的护眼台灯,销售过程中发现,每月销售量y(盏)与销售单价x(元)之间的关系可近似地看作一次函数:y=﹣10x+500.
(1)设每月获得的利润为w(元),求w与x的关系式.
(2)如果想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元.如果童威想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点的坐标分别为A(2,2),B(1,0),C(3,1).

(1)画出△ABC关于x轴对称的△A1BC1,写出点C1的坐标为 ;
(2)画出△ABC绕原点O逆时针旋转90°的△A2B1C2,写出点C2的坐标为 ;
(3)在(1),(2)的基础上,图中的△A1BC1、△A2B1C2关于点 中心对称;
(4)若以点D、A、C、B为顶点的四边形为菱形,直接写出点D的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)图象如图所示,下列结论:①abc>0;②2a+b=0;③a﹣b+c>0;④当x≠1时,a+b>ax2+bx;⑤4ac<b2.其中正确的有( )个
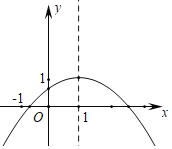
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是⊙O的直径,BA=BC,BD交AC于点E,点F在DB的延长线上,且∠BAF=∠C.
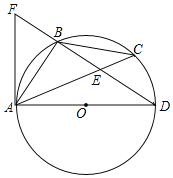
(1)求证:AF是⊙O的切线;
(2)若BC=2![]() ,BE=4,求⊙O半径r.
,BE=4,求⊙O半径r.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com