
【题目】我们用“”表示一种新运算符号,观察下列式子,解决问题:
25=2×2+4=8
34=2×3+3=9
3(﹣1)=2×3﹣2=4
﹣3(﹣5)=2×(﹣3)﹣6=﹣12
……
(1)请你用含a,b的式子表示这个规律:求ab的值;
(2)求(﹣![]() 6)(﹣4)的值;
6)(﹣4)的值;
(3)如果x(﹣3)=3x,求x的值.
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:
【题目】如图,有一块不规则的四边形地皮ABCO,各个顶点的坐标分别为A(-2,6),B(-5,4),C(-7,0),O(0,0)(图上一个单位长度表示10米),现在想对这块地皮进行规划,需要确定它的面积.
(1)求这个四边形的面积;
(2)如果把四边形ABCD的各个顶点的纵坐标保持不变,横坐标加2,所得到的四边形面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在四边形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P从A向点D以1cm/s的速度运动,到点D即停止.点Q从点C向点B以2cm/s的速度运动,到点B即停止.直线PQ将四边形ABCD截得两个四边形,分别为四边形ABQP和四边形PQCD,则当P,Q两点同时出发,几秒后所截得两个四边形中,其中一个四边形为平行四边形? 
查看答案和解析>>
科目:初中数学 来源: 题型:
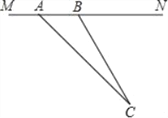
【题目】“为了安全,请勿超速”,如图所示是一条已经建成并通车的公路,且该公路的某直线路段MN上限速17m/s,为了检测来往车辆是否超速,交警在MN旁设立了观测点C.若某次从观测点C测得一汽车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200m.
(1)求观测点C到公路MN的距离;
(2)请你判断该汽车是否超速?(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
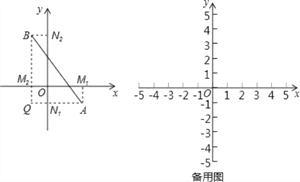
【题目】阅读材料,在平面直角坐标系中,已知x轴上两点A(x1,0),B(x2,0)的距离记作AB=|x1﹣x2|;若A,B是平面上任意两点,我们可以通过构造直角三角形来求AB间的距离,如图,过A,B分别向x轴、y轴作垂线AM1、AN1和BM2、BN2,垂足分别是M1、N1、M2、N2,直线AN1交BM2于点Q,在Rt△ABQ中,AQ=|x1﹣x2|,BQ=|y1﹣y2|,∴AB2=AQ2+BQ2=|x1﹣x2|+|y1﹣y2|2=(x1﹣x2)2+(y1﹣y2)2,由此得到平面直角坐标系内任意两点A(x1,y1),B(x2,y2)间的距离公式为:
(1)AB= .
(2)直接应用平面内两点间距离公式计算点A(1,﹣3),B(﹣2,1)之间的距离为 ;
(3)根据阅读材料并利用平面内两点间的距离公式,求代数式![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个自然数的立方,可以分裂成若干个连续奇数的和,例如:23,33和43分别可以按如图所示的方式“分裂”,则63“分裂”出的奇数中,最大的奇数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线CD与EF相交于点O,∠COE=60°,将一直角三角尺AOB的直角顶点与O重合,OA平分∠COE.
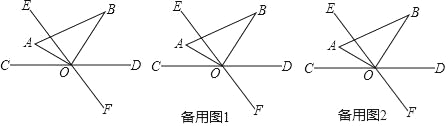
(1)求∠BOD的度数;
(2)将三角尺AOB以每秒3°的速度绕点O顺时针旋转,同时直线EF也以每秒9°的速度绕点O顺时针旋转,设运动时间为t秒(0≤t≤40).
①当t为何值时,直线EF平分∠AOB;
②若直线EF平分∠BOD,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网上购物已经成为人们常用的一种购物方式,售后评价特别引人关注,为了解市民对售后评价的关注情况,随机采访部分市民,对采访情况制作了如下统计图表:
关注情况 | 频数 | 频率 |
A.高度关注 | 50 | b |
B.一般关注 | 120 | 0.6 |
C.不关注 | a | 0.1 |
D.不知道 | 10 | 0.05 |
(1)根据上述统计图可得此次采访的人数为人,a= , b=;
(2)根据以上信息补全条形统计图; 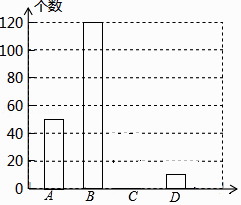
(3)根据上述采访结果,请估计在6400名市民中,高度关注售后评价的市民约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com