Question

【题目】已知点A（1，1），B（－1，1），C（0，4）.

（1）在平面直角坐标系中描出A，B，C三点；

（2）在同一平面内，点与三角形的位置关系有三种：点在三角形内、点在三角形边上、 点在三角形外.若点P在△ABC外，请判断点P关于y轴的对称点P′与△ABC的位置关系，直接写出判断结果.

Answer 1

【答案】（1）答案见详解；（2）点P′在△ABC外.

【解析】

（1）根据点坐标直接在坐标系中描点即可；

（2）分别判断不同区域内点P的位置即可得到点P’的位置，再利用对称性判断与△ABC的位置关系.

（1）如图，

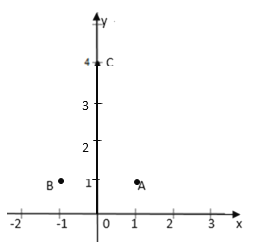
（2）连接AB、AC、BC,由A、B、C三点的位置得：△ABC关于y轴对称，

∵点P在△ABC外，

∴点P可在点C上方的位置，直线AB下方的位置，也可在线段BC、AC外，

若点P可在点C上方的位置，直线AB下方的位置，则点P关于y轴的对称点P′也在该位置，即点P′在△ABC外；

若点P在线段BC、AC外，则点P到y轴的距离大于线段BC、AC上的点到y轴的距离，故点P关于y轴的对称点P′到y轴的距离大于线段AC或BC上的点到y轴的距离，故点P′在△ABC外.