
| A. | $\frac{-a+5}{-a-5}=\frac{a+5}{a-5}$ | B. | $\frac{1}{-x+6}=\frac{-1}{x+6}$ | ||
| C. | $\frac{-x+y}{-x-y}=-\frac{x-y}{x+y}$ | D. | $\frac{-x}{y-3x}=\frac{x}{3x-y}$ |
科目:初中数学 来源: 题型:选择题
| A. | 2.6×103 | B. | 2.6×104 | C. | 2.6×105 | D. | 26×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:图①、图②都是4×4的正方形网格,小正方形的边长均为1,每个小正方形的顶点称为格点.在①、②两个网格中分别标注了5个格点,按下列要求画图:
如图:图①、图②都是4×4的正方形网格,小正方形的边长均为1,每个小正方形的顶点称为格点.在①、②两个网格中分别标注了5个格点,按下列要求画图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 问题提出:如图,已知:线段AB,试在平面内找到符合条件的所有点C,使∠ACB=30°.(利用直尺和圆规作图,保留作图痕迹,不写作法).
问题提出:如图,已知:线段AB,试在平面内找到符合条件的所有点C,使∠ACB=30°.(利用直尺和圆规作图,保留作图痕迹,不写作法).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
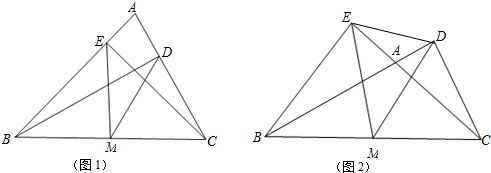
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
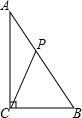 如图,在△ABC中,已知∠ACB=90°,AB=10cm,AC=8cm,动点P从点A出发,以2cm/s的速度沿线段AB向点B运动.在运动过程中,当△APC为等腰三角形时,点P出发的时刻t可能的值为( )
如图,在△ABC中,已知∠ACB=90°,AB=10cm,AC=8cm,动点P从点A出发,以2cm/s的速度沿线段AB向点B运动.在运动过程中,当△APC为等腰三角形时,点P出发的时刻t可能的值为( )| A. | 5 | B. | 5或8 | C. | $\frac{5}{2}$ | D. | 4或$\frac{5}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com