
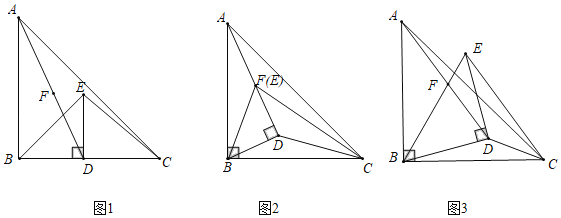
【题目】如图,在△ABC中,∠ABC=90°,AB=BC,点D为BC边上任意一点(与B、C不重合),以BD为直角边构造等腰直角三角形BDE,F为AD的中点.
(1)将△BDE绕点B旋转,当点E与F重合时,求证:∠BAE+∠BCD=45°.
(2)将△BDE绕点B旋转,当点F在BE上且AB=AD时,求证:2CD=BE.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)如图2中,利用等腰直角三角形的性质及旋转的性质,证明△ABF≌△BCD(SAS)即可解决问题.
(2)如图3中,作AN⊥BM于N交BE于G,CM⊥BD于M.只要证明△CDM是等腰直角三角形,BN=DN=DM,即可解决问题.
(1)证明:如图2中,
∵△BDE是等腰直角三角形,△BDE绕点B旋转,当点E与F重合,
∴△BFD是得把直角三角形,
∴∠DBF=∠BFD=45°,BD=DF,
∵F为AD的中点,
∴AF=DF,
∴BD=AF,
∵∠ABC=90°,
∴∠ABF+∠DBC=∠ABF+∠BAF=45°,
∴∠BAF=∠DBC,
∵AB=BC,
∴△ABF≌△BCD(SAS),
∴ABF=∠BCD,
∴∠BAE+∠BCD=45°;
(2)证明:如图3中,作AN⊥BM于N交BE于G,CM⊥BD于M.

由(1)可知△CBM≌△BAN,
∴BN=CM,AN=BM,
∵AB=AD,AN⊥BD,
∴BN=DN,∵ED⊥BD,
∴AN∥DE,
∴∠GAF=∠FDE,BG=GE,
∴DE=2GN,
在△AGF和△DEF中,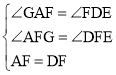 ,
,
∴△AGF≌△DEF(AAS),
∴AG=DE=BD,
∴AN=3BN,BM=3CM,
∵BN=DN,
∴DM=CM,
∴△CDM是等腰直角三角形,
∴CD=![]() CM,
CM,
∵CM=BN=![]() BD,
BD,
∴CD=![]() BD,
BD,
∵BE=![]() BD,
BD,
∴BE=2CD.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.

(1)概念理解:
如图1,在△ABC中,AC=6,BC=3,∠ACB=30°,试判断△ABC是否是”等高底”三角形,请说明理由.
(2)问题探究:
如图2,△ABC是“等高底”三角形,BC是”等底”,作△ABC关于BC所在直线的对称图形得到△A'BC,连结AA′交直线BC于点D.若点B是△AA′C的重心,求![]() 的值.
的值.
(3)应用拓展:
如图3,已知l1∥l2,l1与l2之间的距离为2.“等高底”△ABC的“等底”BC在直线l1上,点A在直线l2上,有一边的长是BC的![]() 倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.
倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线![]() 经过点M(1,3)和N(3,5)
经过点M(1,3)和N(3,5)

(1)试判断该抛物线与x轴交点的情况;
(2)平移这条抛物线,使平移后的抛物线经过点A(﹣2,0),且与y轴交于点B,同时满足以A、O、B为顶点的三角形是等腰直角三角形,请你写出平移过程,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑摩托车从B地到A地,到达A地后立即按原路返回.如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
(1)直接写出y甲,y乙与x之间的函数关系式(不写过程);
(2)①求出点M的坐标,并解释该点坐标所表示的实际意义;
②根据图象判断,x取何值时,y乙>y甲.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】六一期间,某公园游戏场举行“迎奥运”活动.有一种游戏的规则是:在一个装有![]() 个红球和若干个白球(每个球除颜色外其他相同)的袋中,随机摸一个球,摸到一个红球就得到一个奥运福娃玩具.已知参加这种游戏活动为
个红球和若干个白球(每个球除颜色外其他相同)的袋中,随机摸一个球,摸到一个红球就得到一个奥运福娃玩具.已知参加这种游戏活动为![]() 人次,公园游戏场发放的福娃玩具为
人次,公园游戏场发放的福娃玩具为![]() 个.
个.
![]() 求参加一次这种游戏活动得到福娃玩具的概率;
求参加一次这种游戏活动得到福娃玩具的概率;
![]() 请你估计袋中白球接近多少个?
请你估计袋中白球接近多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区商店以2元的批发价进了一批纪念品.经调查发现,每个定价3元,每天可以能卖出500件,而且定价每上涨0.1元,其销售量将减少10件.根据规定:纪念品售价不能超过批发价的2.5倍.
(1)当每个纪念品定价为3.5元时,商店每天能卖出________件;
(2)如果商店要实现每天800元的销售利润,那该如何定价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 分别表示
分别表示![]() 步行与
步行与![]() 骑车在同一路上行驶的路程
骑车在同一路上行驶的路程![]() (千来)与时间
(千来)与时间![]() (小时)之间的关系.
(小时)之间的关系.
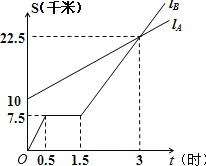
(1)![]() 出发时与
出发时与![]() 相距______千米.
相距______千米.
(2)![]() 走了一段路后,自行车发生故障,进行修理,所用的时间是______小时.
走了一段路后,自行车发生故障,进行修理,所用的时间是______小时.
(3)![]() 出发后______小时与
出发后______小时与![]() 相遇.
相遇.
(4)求出![]() 行走的路程
行走的路程![]() 与时间
与时间![]() 的函数关系式.
的函数关系式.
(5)若![]() 的自行车不发生故障,保持出发时的速度前进,那么几小时与
的自行车不发生故障,保持出发时的速度前进,那么几小时与![]() 相遇?相遇点离
相遇?相遇点离![]() 的出发点多少千米?请同学们在图中画出这个相遇点
的出发点多少千米?请同学们在图中画出这个相遇点![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
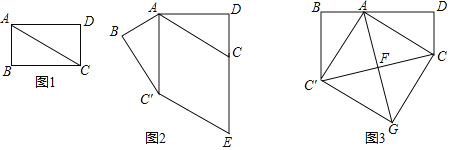
【题目】如图1,将矩形纸片ABCD沿AC剪开,得到△ABC和△ACD.
(1)将图1中的△ABC绕点A顺时针旋转∠α,使∠α=∠BAC,得到图2所示的△ABC′,过点C′作C′E∥AC,交DC的延长线于点E,试判断四边形ACEC′的形状,并说明理由.
(2)若将图1中的△ABC绕点A顺时针旋转,使B,A,D在同一条直线上,得到图3所示的△ABC′,连接CC′,过点A作AF⊥CC′于点F,延长AF至点G,使FG=AF,连接CG,C′G,试判断四边形ACGC′的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,已知AD⊥BC,∠B=64°,∠C=56°,
(1)求∠BAD和∠DAC的度数;
(2)若DE平分∠ADB,求∠AED的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com