Question

3．如图①，在平面直角坐标系中，点M在x轴正半轴上，⊙M交x轴于A、B两点，交y轴于C、D两点，且C为$\widehat{AE}$的中点，连结CE、AE、CB、EB，AE与y轴交于点F，已知A（-2，0），C（0，4）．
（1）求证：AF=CF；
（2）求⊙M的半径及EB的长；
（3）如图②，P为x轴下方半圆弧上的动点，连结PE交CB于R，当△CRE为等腰三角形时，直接写出EP的长．

Answer 1

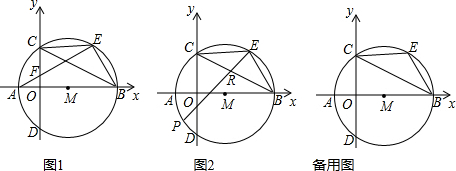
分析 （1）如图1所示：连结AC．证明$\widehat{AD}=\widehat{AC}=\widehat{CE}$，从而可得到∠ACD=∠CAE，故此AF=CF；
（2）如图2所示：连结AC、AD、CM，CM交AE于H．设半径为x，则OM=x-2，在△COM中由勾股定理可求得x=5，然后在△ACM中利用面积法求得AH=4，从而得到AE=8，最后在△AEB中，由勾股定理求得BE=6；
（3）如图3所示：当ER=CR时，证明△PCE≌△BCE，从而得打PE=BC=4$\sqrt{5}$；如图4所示：CE=CR时．过点B作BN⊥EP，垂足为N．先证明△EBN为等腰直角三角形，在△BEN中利用特殊锐角三角函数可求得EN=3$\sqrt{2}$，然后根据△AEB∽△PNB可求得NP=4$\sqrt{2}$；如图6所示：当CE=ER=2$\sqrt{3}$时．过点E作EG⊥BC，垂足为G．先证明△CEG∽△AEB，从而可求得CG=4，于是可得到CR=8，BR=4$\sqrt{5}$-8，接下来证明△AER∽△BPR，从而可求得PR=$\frac{80-32\sqrt{5}}{5}$，故可求得EP=$\frac{80-22\sqrt{5}}{5}$．

解答 解：（1）如图1所示：连结AC．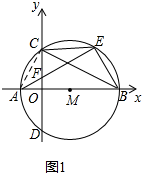

∵C是$\widehat{AE}$的中点，
∴$\widehat{AC}=\widehat{CE}$，
∴AC=CE，
∴∠CAE=∠AEC，
∵AB是直径，AB⊥CD，
∴AC=AD，
∴∠ACD=∠ADC=∠AEC，
∴∠ACD=∠CAE，
∴AF=CF；
（2）如图2所示：连结AC、AD、CM，CM交AE于H．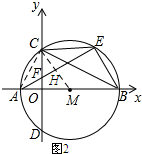

由题意得：OC=4，OA=2，设半径为x，则OM=x-2，
∴（x-2）²+4²=x²．
解得：x=5，
∴M（3，0）．
∴圆M的半径=OM+OA=3+2=5
∵点C是弧AE的中点，
∴AC=CE．
∴CM⊥AE，AE=2AH．
∵S_△ACM=$\frac{1}{2}$CM•AH=$\frac{1}{2}$AM•OC，CM=AM，
∴AH=OC=4．
∴AE=8．
∵AB=2×5=10，
∴EB=$\sqrt{A{B}^{2}-A{E}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6；
（3）如图3所示：当ER=CR时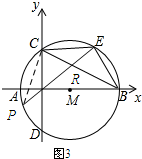

∵ER=CR，
∴∠ECB=∠CEP．
在△PCE和△BCE中，
$\left\{\begin{array}{l}{∠CBE=∠EPC}\\{∠ECB=∠CEP}\\{CE=CE}\end{array}\right.$，
∴EP=CB=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$；
如图4所示：CE=CR时．过点B作BN⊥EP，垂足为N．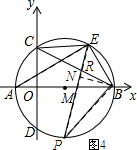

∵CE=CR，
∴∠CER=∠CRE．
∴∠PEB+∠EBC=∠CEA+∠AEP．
又∵点C是弧AE的中点，
∴∠CBE=∠CEA．
∴∠AEP=∠BEP．
又∵∠AEP+∠BEP=90°．
∴∠AEP=∠BEP=45°．
∵在△EBN中，BE=6，∠ENB=90°，∠NEB=45°，
∴NB=NE=6×$\frac{\sqrt{2}}{2}$=3$\sqrt{2}$．
∵∠EAB=∠NPB，∠AEB=∠BNP=90°，
∴△AEB∽△PNB．
∴$\frac{NB}{NP}=\frac{EB}{AE}$，即$\frac{3\sqrt{2}}{NP}=\frac{6}{8}$．
∴NP=4$\sqrt{2}$．
∴EP=3$\sqrt{2}+4\sqrt{2}$=7$\sqrt{2}$．
如图6所示：当CE=ER=2$\sqrt{5}$时．过点E作EG⊥BC，垂足为G．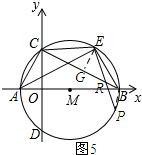

在Rt△COB中，BC=$\sqrt{O{C}^{2}+O{B}^{2}}$=4$\sqrt{5}$．
∵∠ECB=∠EAB，∠AEB=∠CGE=90°，
∴△CEG∽△ABE．
∴$\frac{CE}{AB}=\frac{CG}{AE}$，即$\frac{2\sqrt{5}}{10}=\frac{CG}{8}$．
解得：CG=$\frac{8\sqrt{5}}{5}$．
∴CR=$\frac{16\sqrt{5}}{5}$．
∴BR=4$\sqrt{5}$-$\frac{16\sqrt{5}}{5}$=$\frac{4\sqrt{5}}{5}$．
∵∠BPE=∠ECR，∠ERC=∠BRP，
∴△AER∽△BPR．
∴$\frac{BR}{CE}=\frac{PR}{CR}$，即$\frac{\frac{4\sqrt{5}}{5}}{2\sqrt{5}}=\frac{PR}{\frac{16\sqrt{5}}{5}}$．
解得：PR=$\frac{32\sqrt{5}}{25}$．
∴EP=2$\sqrt{5}$+$\frac{32\sqrt{5}}{25}$=$\frac{82\sqrt{5}}{25}$．
综上所述，EP的长度为4$\sqrt{5}$或7$\sqrt{2}$或$\frac{82\sqrt{5}}{25}$．

点评 本题主要考查的是圆的综合应用，解答本题主要应用了相似三角形的性质和判定、全等三角形的性质和判定、勾股定理，垂径定理、圆周角定理，根据题意画出符合题意的图形是解题的关键．