练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知△ABC的两条中线的长分别为5、10，若第三条中线的长也是整数，则第三条中线长的最大值（ ）

    A.7B.8C.14D.15

    【答案】C

    【解析】

    如图，角A、B、C对应的中点分别是D、E、F，且三条中线交点是O，将OD延长到G，使OD=DG，连接BG，设BE=5,CF=10，AD则为第三条中线长，根据三角形的三边关系和中线的性质列出不等式组，即可求出第三条中线长的最大值．

    如图，角A、B、C对应的中点分别是D、E、F，且三条中线交点是O，将OD延长到G，使OD=DG，连接BG，设BE=5,CF=10，AD则为第三条中线长

    ∵角A、B、C对应的中点分别是D、E、F，且三条中线交点是O

    ∴，

    ∵OD=DG

    ∴

    ∴

    ∴

    ∴

    ∵第三条中线的长也是整数

    ∴第三条中线长的最大值为14

    故答案为：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】文化是一个国家、一个民族的灵魂，近年来，央视推出《中国诗词大会》、《中国成语大会》、《朗读者》、《经曲咏流传》等一系列文化栏目．为了解学生对这些栏目的喜爱情况，某学校组织学生会成员随机抽取了部分学生进行调查，被调查的学生必须从《经曲咏流传》（记为A）、《中国诗词大会》（记为B）、《中国成语大会》（记为C）、《朗读者》（记为D）中选择自己最喜爱的一个栏目，也可以写出一个自己喜爱的其他文化栏目（记为E）．根据调查结果绘制成如图所示的两幅不完整的统计图．

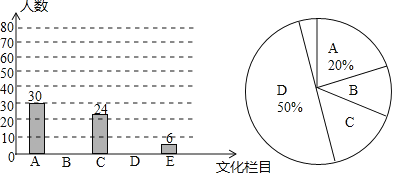
    请根据图中信息解答下列问题：

    （1）在这项调查中，共调查了多少名学生？

    （2）将条形统计图补充完整，并求出扇形统计图中“B”所在扇形圆心角的度数；

    （3）若选择“E”的学生中有2名女生，其余为男生，现从选择“E”的学生中随机选出两名学生参加座谈，请用列表法或画树状图的方法求出刚好选到同性别学生的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知直线与抛物线： 相交于和点两点.

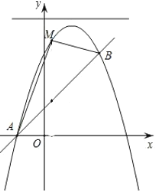
    ⑴求抛物线的函数表达式；

    ⑵若点是位于直线上方抛物线上的一动点，以为相邻两边作平行四边形,当平行四边形的面积最大时，求此时四边形的面积及点的坐标；

    ⑶在抛物线的对称轴上是否存在定点,使抛物线上任意一点到点的距离等于到直线的距离，若存在，求出定点的坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】随机抛掷图中均匀的正四面体(正四面体的各面依次标有1，2，3，4四个数字)，并且自由转动图中的转盘(转盘被分成面积相等的五个扇形区域)．

    （1） 请用列表法或树状图法的方法求正四面体着地的数字与转盘指针所指区域的数字之和为6的概率；

    （2）设正四面体着地的数字为a，转盘指针所指区域内的数字为b，求关于x的方程ax2-4x＋＝0有实数根的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图：直线AB与双曲线y点交于A、B两点，直线AB与x、y坐标轴分别交于C、D两点，连接OA，若OA＝2，tan∠AOC，B（3，m）

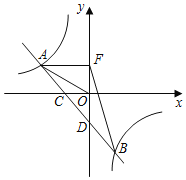
    （1）求一次函数与反比例函数解析式；

    （2）若点F是点D关于x轴的对称点，求△ABF的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，一块含60°角的三角板作如图摆放，斜边AB在x轴上，直角顶点C在y轴正半轴上，已知点A（﹣1，0）．

    （1）请直接写出点B、C的坐标：B（ ）、C（ ）；并求经过A、B、C三点的抛物线解析式；

    （2）现有与上述三角板完全一样的三角板DEF（其中∠EDF=90°，∠DEF=60°），把顶点E放在线段AB上（点E是不与A、B两点重合的动点），并使ED所在直线经过点C．此时，EF所在直线与（1）中的抛物线交于点M．

    ①设AE=x，当x为何值时，△OCE∽△OBC；

    ②在①的条件下探究：抛物线的对称轴上是否存在点P使△PEM是等腰三角形？若存在，请写出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB＝AC，以AB为直径的⊙O交BC于点D，过点D作EF⊥AC于点E，交AB延长线于点F．

    （1）判断直线EF与⊙O的位置关系，并说明理由；

    （2）若⊙O半径为5，CD＝6，求DE的长；

    （3）求证：BC2＝4CEAB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，A，B两地被池塘隔开，小明通过下列方法测出了A、B间的距离：先在AB外选一点C，然后测出AC，BC的中点M，N，并测量出MN的长为12m，由此他就知道了A、B间的距离．有关他这次探究活动的描述错误的是（ ）

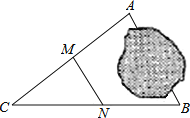
    A. AB=24m B. MN∥AB

    C. △CMN∽△CAB D. CM：MA=1：2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】学校准备在各班设立图书角以丰富同学们的课余文化生活，为了更合理的搭配各类书籍，学校团委以“我最喜爱的书籍”为主题，对学生最喜爱的一种书籍类型进行随机抽样调查，收集整理数据后，绘制出以下两幅未完成的统计图，请根据图1和图2提供的信息，解答下列问题：

    （1）在这次抽样调查中，一共调查了多少名学生？

    （2）请把折线统计图（图1）补充完整；

    （3）求出扇形统计图（图2）中，体育部分所对应的圆心角的度数；

    （4）如果这所中学共有学生1800名，那么请你估计最喜爱科普类书籍的学生人数．

    （5）学校若在喜爱艺术、文学、科普、体育四类中任意抽取两类建立兴趣小组，求出恰好选中是体育和科普两类的概率？

    查看答案和解析>>

    同步练习册答案