
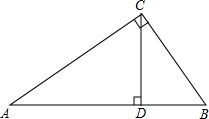
 如图,在Rt△ACB中,∠ACB=90°,CD⊥AB于点D,则tanA=$\frac{BC}{AC}$=$\frac{CD}{AD}$,tanB=$\frac{AC}{BC}$=$\frac{CD}{BD}$,tan∠ACD=tanB,tan∠BCD=tanA.
如图,在Rt△ACB中,∠ACB=90°,CD⊥AB于点D,则tanA=$\frac{BC}{AC}$=$\frac{CD}{AD}$,tanB=$\frac{AC}{BC}$=$\frac{CD}{BD}$,tan∠ACD=tanB,tan∠BCD=tanA. 分析 先由三角形的高的定义得出∠ADC=∠CDB=90°,在Rt△ACB与Rt△ACD中根据正切函数的定义求出tanA的值,在Rt△ACB与Rt△BCD中根据正切函数的定义求出tanB的值;再根据直角三角形及余角的性质求出∠ACD=∠B,∠BCD=∠A,进而求解即可.
解答 解:∵CD⊥AB于点D,
∴∠ADC=∠CDB=90°,
∵在Rt△ACB中,∠ACB=90°,
∴tanA=$\frac{BC}{AC}$=$\frac{CD}{AD}$,tanB=$\frac{AC}{BC}$=$\frac{CD}{BD}$;
∵∠A+∠B=90°,
∠A+∠ACD=90°,
∠B+∠BCD=90°,
∴∠ACD=∠B,∠BCD=∠A,
∴tan∠ACD=tanB=$\frac{AC}{BC}$=$\frac{CD}{BD}$,tan∠BCD=tanA=$\frac{BC}{AC}$=$\frac{CD}{AD}$.
故答案为$\frac{BC}{AC}$,$\frac{CD}{AD}$,$\frac{AC}{BC}$,$\frac{CD}{BD}$,tanB,tanA.
点评 本题考查了解直角三角形,三角形的高,锐角三角函数的定义,直角三角形及余角的性质,比较简单.掌握正切函数的定义是解题的关键.


科目:初中数学 来源: 题型:选择题
 如图,一个机器人从O点出发,向正东方向走3米到达A1点,再向正北方向走6米到达A2点,再向正西方向走9米到达A3点,再向正南方向走12米到达A4点,再向正东方向走15米到达A5点,按如此规律走下去,当机器人走到A6点时,则A6的坐标为( )
如图,一个机器人从O点出发,向正东方向走3米到达A1点,再向正北方向走6米到达A2点,再向正西方向走9米到达A3点,再向正南方向走12米到达A4点,再向正东方向走15米到达A5点,按如此规律走下去,当机器人走到A6点时,则A6的坐标为( )| A. | (9,15) | B. | (6,15) | C. | (9,9) | D. | (9,12) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
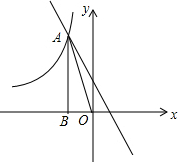 如图,Rt△ABO中,顶点A是双曲线y=$\frac{k}{x}$与直线y=-x-(k+1)在第二象限的交点,AB⊥x轴于点B,且S△AOB=$\frac{3}{2}$,求这两个函数的解析式.
如图,Rt△ABO中,顶点A是双曲线y=$\frac{k}{x}$与直线y=-x-(k+1)在第二象限的交点,AB⊥x轴于点B,且S△AOB=$\frac{3}{2}$,求这两个函数的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 14°38′ | B. | 65°22′ | C. | 67°23′ | D. | 22°37′ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 地震发生后,一支专业搜救队驱车前往灾区救援.如图,汽车在一条南北走向的公路上向北行驶,当在A处时,车载GPS(全球卫星定位系统)显示村庄C在北偏西26°方向,汽车以35km/h的速度前行2h到达B处,GPS显示村庄在北偏西52°方向.
地震发生后,一支专业搜救队驱车前往灾区救援.如图,汽车在一条南北走向的公路上向北行驶,当在A处时,车载GPS(全球卫星定位系统)显示村庄C在北偏西26°方向,汽车以35km/h的速度前行2h到达B处,GPS显示村庄在北偏西52°方向.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 都不变 | B. | 都扩大2倍 | C. | 都缩小$\frac{1}{2}$ | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com