Question

3．边长为3的正六边形的面积为$\frac{27\sqrt{3}}{2}$．

Answer 1

分析 根据题意画出图形，边长为3的正六边形可以分成六个边长为3的正三角形，计算出正六边形的面积即可．

解答 解：如图，连接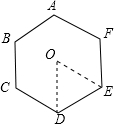OD，OE，
∵∠DOE=360°×$\frac{1}{6}$=60°，
又∵OD=OE，
∴∠ODE=∠OED=（180°-60°）÷2=60°，
∴三角形ODE为正三角形，
∴OD=OE=DE=3，
∴S_△ODE=$\frac{1}{2}$OD•OE•sin60°=$\frac{1}{2}$×3×3×$\frac{\sqrt{3}}{2}$=$\frac{9\sqrt{3}}{4}$．
∴正六边形的面积=6×$\frac{9\sqrt{3}}{4}$=$\frac{27\sqrt{3}}{2}$．
故答案为：$\frac{27\sqrt{3}}{2}$．

点评 本题考查的是正多边形和圆，根据题意画出图形，构造出等边三角形是解答此题的关键．