
分析 根据(ax-4)(3x+n)计算结果为-6x2+mx-20,可以将(ax-4)(3x+n)展开,然后找准和-6x2+mx-20对应的量,即可求得a、n、m的值,本题得以解决.
解答 解:∵(ax-4)(3x+n)计算结果为-6x2+mx-20,
∴(ax-4)(3x+n)=-6x2+mx-20,
∴3ax2+(an-12)x-4n=-6x2+mx-20,
∴$\left\{\begin{array}{l}{3a=-6}\\{an-12=m}\\{-4n=-20}\end{array}\right.$
解得,$\left\{\begin{array}{l}{a=-2}\\{n=5}\\{m=-22}\end{array}\right.$
故答案为:-2,5,-22.
点评 本题考查多项式乘以多项式,解题的关键是明确题意,找准对应关系.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:解答题
| 精品盒数量(盒) | 普通盒数量(盒) | 合计(盒) | |
| 甲店 | a | 30-a | 30 |
| 乙店 | 35-a | a-5 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
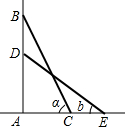 如图,一架梯子斜靠在墙上,梯子与地面的夹角为a(a=∠BCA),当梯顶下滑1m时,这架梯子与地面的夹角为b(b=∠DEA,A、C、E三点在一条直线上),求梯子的长.
如图,一架梯子斜靠在墙上,梯子与地面的夹角为a(a=∠BCA),当梯顶下滑1m时,这架梯子与地面的夹角为b(b=∠DEA,A、C、E三点在一条直线上),求梯子的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≥$\frac{1}{2}$ | B. | x≤$\frac{1}{2}$ | C. | x>$\frac{1}{2}$ | D. | x<$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com