
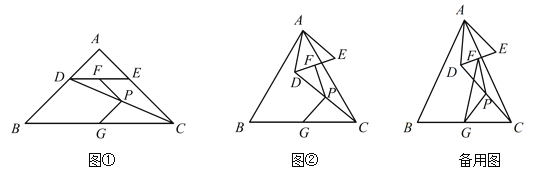
【题目】在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]()
![]() ,点
,点![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 的中点,连接
的中点,连接![]() ,
,![]() .
.
(1)如图①,![]() ,点
,点![]() 在
在![]() 上,则
上,则![]()
![]() ;
;
(2)如图②,![]() ,点
,点![]() 不在
不在![]() 上,判断
上,判断![]() 的度数,并证明你的结论;
的度数,并证明你的结论;
(3)连接![]() ,若
,若![]() ,
,![]() ,固定
,固定![]() ,将
,将![]() 绕点
绕点![]() 旋转,当
旋转,当![]() 的长最大时,
的长最大时,![]() 的长为 (用含
的长为 (用含![]() 的式子表示).
的式子表示).
【答案】(1)![]() ;(2)
;(2)![]() ,证明见解析;(3)
,证明见解析;(3)![]()
【解析】
(1)由AB=AC、AD=AE,得BD=CE,再根据G、P、F分别是BC、CD、DE的中点,可得出PG∥BD,PF∥CE.则∠GPF=180°—![]() =90°;
=90°;
(2)连接BD,连接CE,由已知可证明△ABD≌△ACE,则∠ABD=∠ACE.因为G、P、F分别是BC、CD、DE的中点,则PG∥BD,PF∥CE.进而得出∠GPF=180°—![]() =120°;
=120°;
(3)当D在BA的延长线上时,CE=BD最长,此时BD=AB+AD=5+2=7,再由三角形中位线定理即可算出PG=3.5,在Rt△GPH中,由三角函数的定义即可求出GH,进一步求出FG.
解:(1)∵AB=AC、AD=AE,
∴BD=CE,
∵G、P、F分别是BC、CD、DE的中点,
∴PG∥BD,PF∥CE.
∴∠ADC=∠DPG,∠DPF=∠ACD,
∴∠GPF=∠DPF+∠DPG=∠ADC+∠ACD=180°-∠BAC=![]() =90°,
=90°,
即∠GPF=90°;
(2)∠FPG=120°,证明如下:
如图,连接BD,连接CE.如图②,
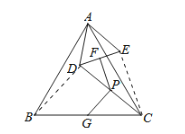
∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
 ,
,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
∵G、P、F分别是BC、CD、DE的中点,
∴PG∥BD,PF∥CE,
∴∠PGC=∠CBD,
∠DPF=∠DCE=∠DCA+∠ACE=∠DCA+∠ABD,
∠DPG=∠PGC+∠BCD=∠CBD+∠BCD,
∴∠GPF=∠DPF+∠DPG=∠DCA+∠ABD+∠CBD+∠BCD=180°—∠BAC=180°—![]() =120°,
=120°,
即∠GPF=120°;
(3)如图,连结BD,CE,过P作PH⊥FG于H,
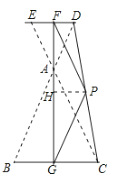
由(2)可知,△ABD≌△ACE,
∴BD=CE,且![]() ,
,
当D在BA的延长线上时,CE最长,即BD最长,此时BD=AB+AD=5+2=7,
∴PG=3.5,
∵PF=PG,PH⊥FG,
∴![]() ,
,![]() FG=2HG,
FG=2HG,
∴![]() ,
,
故答案为:![]() .
.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:初中数学 来源: 题型:
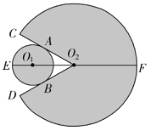
【题目】某玩具由一个圆形区域和一个扇形区域组成,如图,在⊙O1和扇形O2CD中,⊙O1与O2C、O2D分别切于点A、B,已知∠CO2D=60°,E、F是直线O1O2与⊙O1、扇形O2CD的两个交点,且EF=24cm,设⊙O1的半径为xcm,
(1)用含x的代数式表示扇形O2CD的半径;
(2)若⊙O1和扇形O2CD两个区域的制作成本分别为0.45元/cm2和0.06元/cm2,当⊙O1的半径为多少时,该玩具的制作成本最小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小章为学校举办的数学文化节没计的标志,在△ABC中,∠ACB=90°,以△ABC的各边为边作三个正方形,点G落在HI上,若AC+BC=6,空自部分面积为10.5,则阴影部分面积为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校八年级体育科目训练情况,从八年级学生中随机抽取了部分学生进行了一次体育科目测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图![]() 请根据统计图中的信息解答下列问题:
请根据统计图中的信息解答下列问题:

(1)图1中![]() 的度数是__________,并把图2条形统计图补充完整.
的度数是__________,并把图2条形统计图补充完整.
(2)抽取的这部分的学生的体育科目测试结果的中位数是在__________级;
(3)依次将优秀、良好、及格、不及格记为90分、80分、70分、50分,请计算抽取的这部分学生体育的平均成绩.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l1:y=k1x+b过A(0,﹣3),B(5,2),直线l2:y=k2x+2.
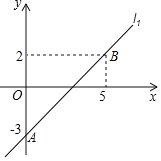
(1)求直线l1的表达式;
(2)当x≥4时,不等式k1x+b>k2x+2恒成立,请写出一个满足题意的k2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了调查学生预防“新型冠状病毒”知识的情况,在全校随机抽取了一部分学生进行民意调查,调查结果分为A.B.C三个等级,其中A:非常了解,B:了解,C:不了解,并根据调查结果绘制了如下两个不完整的统计图,请根据统计图,解答下列问题:

(1)这次抽查的学生为 人;
(2)求等级A在扇形统计图中所占圆心角的度数;
(3)若该校有学生2200人,请根据抽样调查的结果,估计该校约有多少学生对预防新型冠状病毒知识已经了解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市组织全民健身活动,有100名男选手参加由跑、跳、投等10个田径项目组成的“十项全能”比赛.其中25名选手的一百米跑成绩排名,跳远成绩排名与10项总成绩的排名情况如图所示,
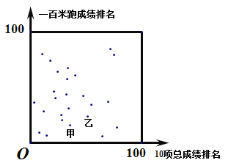
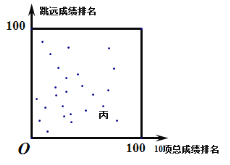
甲、乙、丙表示三名男选手,下面有3个推断:
①甲的一百米跑成绩排名比10项总成绩排名靠前;②乙的一百米跑成绩排名比10项总成绩排名靠后;③丙的一百米跑成绩排名比跳远成绩排名靠前.
其中合理的是( )
A.③B.①C.①③D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市某特产专卖店销售一种蜜枣,每千克的进价为10元,销售过程中发现,每天销量![]() 与销售单价x(元)之间关系可以近似地看作一次函数
与销售单价x(元)之间关系可以近似地看作一次函数![]() .(利润=售价-进价)
.(利润=售价-进价)
(1)写出每天的利润w(元)与销售单价x(元)之间函数解析式;
(2)当销售单价定为多少元时,这种蜜枣每天能够获得最大利润?最大利润是多少元?
(3)物价部门规定,这种蜜枣的销售单价不得高于30元.若商店想要这种蜜枣每天获得300元的利润,则销售单价应定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com