
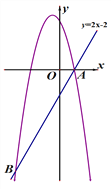
【题目】已知直线y=2x-2与抛物线![]() 交于点A(1,0)和点B,且m<n.
交于点A(1,0)和点B,且m<n.
(1)当m=![]() 时,直接写出该抛物线顶点的坐标.
时,直接写出该抛物线顶点的坐标.
(2)求点B的坐标(用含m的代数式表示).
(3)设抛物线顶点为C,记△ABC的面积为S.
①![]() ,求线段AB长度的取值范围;
,求线段AB长度的取值范围;
②当![]() 时,求对应的抛物线的函数表达式
时,求对应的抛物线的函数表达式
【答案】(1)(﹣![]() ,
,![]() );(2)B点坐标为(
);(2)B点坐标为(![]() ﹣2,
﹣2,![]() ﹣6);(3)①5
﹣6);(3)①5![]() ≤AB≤9
≤AB≤9![]() ;②
;②![]() 或
或![]()
【解析】试题分析:
(1)把点A(1,0)代入![]() 中可得n=-2m,结合m=-2可得二次函数的解析式,再配方即可求得其图象的顶点坐标了;
中可得n=-2m,结合m=-2可得二次函数的解析式,再配方即可求得其图象的顶点坐标了;
(2)联立一次函数和二次函数的解析式组成方程组,解方程组即可求得点B的坐标;
(3)①由(2)中所得点B的坐标结合点A的坐标可用含m的代数式表达出AB2=![]() ,由
,由![]() 可得
可得![]() ,这样即可得到AB2在
,这样即可得到AB2在![]() 的范围内随着m的增大而减小,将m=-3和m=-1分别代入AB2的表达式即可求得AB2的最大值和最小值,由此即可求得对应的AB的最大值和最小值了,从而可得AB的取值范围;
的范围内随着m的增大而减小,将m=-3和m=-1分别代入AB2的表达式即可求得AB2的最大值和最小值,由此即可求得对应的AB的最大值和最小值了,从而可得AB的取值范围;
②设抛物线的对称轴与直线AB交于点E,由已知条件易得点E的坐标为![]() ,用含m的代数式表达出抛物线的顶点的坐标,这样即可由S=S△CEB+S△ACD=
,用含m的代数式表达出抛物线的顶点的坐标,这样即可由S=S△CEB+S△ACD=![]() ,结合已知条件用列出关于m的方程,解方程即可求得对应的m的值,将所得m的值代入抛物线的解析式中即可求得对应的解析式.
,结合已知条件用列出关于m的方程,解方程即可求得对应的m的值,将所得m的值代入抛物线的解析式中即可求得对应的解析式.
试题解析:
(1)∵抛物线y=mx2+mx+n过点A(1,0),得n=﹣2m,
∴抛物线的解析式为:![]() ,
,
又∵m==-2,
∴抛物线的解析式为![]() ,
,
∴抛物线的顶点坐标为(﹣![]() ,
,![]() );
);
(2)由 ![]() 消去y可得:mx2+(m﹣2)x﹣2m+2=0,
消去y可得:mx2+(m﹣2)x﹣2m+2=0,
即x2+(1﹣![]() )x﹣2+
)x﹣2+![]() =0, 解得x=1或x=
=0, 解得x=1或x=![]() ﹣2,
﹣2,
∴B点坐标为(![]() ﹣2,
﹣2,![]() ﹣6),
﹣6),
(3)①由勾股定理可得AB2=![]() ,
,
∵![]() ,
,
∴ ![]() ,
,
∴AB2随![]() 的增大而减小,
的增大而减小,
∴当![]() =-3时,AB2有最大值405,则AB有最大值
=-3时,AB2有最大值405,则AB有最大值![]() ,
,
当![]() =-1时,AB2有最小值125,则AB有最小值
=-1时,AB2有最小值125,则AB有最小值![]() ,
,
∴线段AB长度的取值范围为![]() ≤AB≤
≤AB≤![]() ;
;
②如下图,设抛物线对称轴交直线AB于点E,
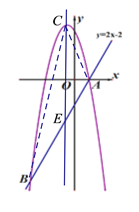
∵抛物线对称轴为x=﹣![]() ,点E在直线AB:y=2x﹣2上,
,点E在直线AB:y=2x﹣2上,
∴E(﹣![]() ,﹣3),
,﹣3),
∵A(1,0),B![]() ,且m<0,设△ABC的面积为S,
,且m<0,设△ABC的面积为S,
∴S=S△CEB+S△ACD=![]() (
(![]() +3)(3-
+3)(3-![]() )=
)=![]() ,解得m=-1或m=
,解得m=-1或m=![]() ,
,
对应的抛物线的函数表达式为![]() 或
或![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】观察下列两个等式:![]() ,
,![]() ,给出定义如下:我们称使等式a﹣b=ab+1的成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对
,给出定义如下:我们称使等式a﹣b=ab+1的成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对![]() ,
,![]() ,都是“共生有理数对”.
,都是“共生有理数对”.
(1)数对![]() ,
,![]() 中是“共生有理数对”的是 ;
中是“共生有理数对”的是 ;
(2)若(m,n)是“共生有理数对”,则(﹣n,﹣m) “共生有理数对”(填“是”或“不是”);
(3)请再写出一对符合条件的“共生有理数对”为 ;(注意:不能与题目中已有的“共生有理数对”重复)
(4)若(a,3)是“共生有理数对”,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,⊙O的直径AB=12,P是弦BC上一动点(与点B,C不重合),∠ABC=30°,过点P作PD⊥OP交⊙O于点D.
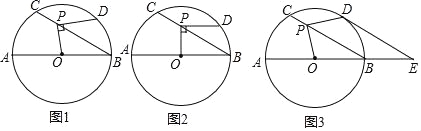
(1)如图2,当PD∥AB时,求PD的长;
(2)如图3,当![]() 时,延长AB至点E,使BE=
时,延长AB至点E,使BE=![]() AB,连接DE.
AB,连接DE.
①求证:DE是⊙O的切线;
②求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】O为直线AB上的一点,OC⊥OD,射线OE平分∠AOD.
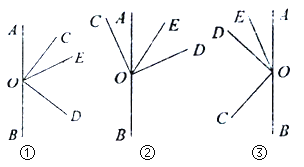
(1)如图①,判断∠COE和∠BOD之间的数量关系,并说明理由;
(2)若将∠COD绕点O旋转至图②的位置,试问(1)中∠COE和∠BOD之间的数量关系是否发生变化?并说明理由;
(3)若将∠COD绕点O旋转至图③的位置,探究∠COE和∠BOD之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
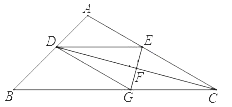
【题目】如图,△ABC中,CD平分∠ACB,CD的垂直平分线分别交AC、DC、BC
于点E、F、G,连接DE、DG.
(1)求证:四边形DGCE是菱形;
(2)若∠ACB=30°,∠B=45°,CG=10,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励市民节约用水,某市自来水公司对每户用水量进行了分段计费,每户每月用水量在规定吨数以下的收费标准相同,规定吨数以上的超过部分收费相同.如表是小明家1-4月
用水量和交费情况,根据表格提供的数据,回答:
月份 | 一 | 二 | 三 | 四 |
用水量(吨) | 6 | 7 | 12 | 15 |
水费(元) | 12 | 14 | 28 | 37 |
(1)该市规定用水量为 吨,规定用量内的收费标准是 元/吨,超过部分的收费标准是 元/吨。
(2)若小明家5月份用水20吨,则应缴水费 元。
(3)若小明家6月份应交水费46元,则6月份他们家的用水量是多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
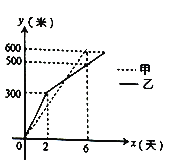
【题目】甲乙两个工程队分别同时开挖两条600米长的管道,所挖管道长度![]() (米)与挖掘时间
(米)与挖掘时间![]() (天)之间的关系如图所示,则下列说法中:
(天)之间的关系如图所示,则下列说法中:
①甲队每天挖100米;②乙队开挖两天后,每天挖50米;③甲队比乙队提前1天完成任务;④当![]() 时,甲乙两队所挖管道长度相同,不正确的个数有( )
时,甲乙两队所挖管道长度相同,不正确的个数有( )
A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
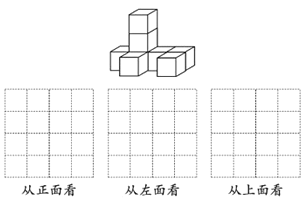
【题目】将8个同样大小的小正方体搭成如图所示的几何体,请按照要求解答下列问题:
(1)从正面、左面、上面观察如图所示的几何体,分别画出所看到的几何体的形状图;
(2)如果在这个几何体上再摆放一个相同的小正方体,并保持这个几何体从上面看和从左面看到的形状图不变.
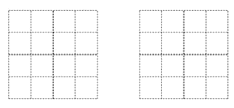
①添加小正方体的方法共有_________种;
②请画出两种添加小正方体后,从正面看到的几何体的形状图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com