

| 6 | 6 | 6 |
| 8 | 8 | 8 |
| 10 | 10 | 10 |
分析 (1)读题意,按照口诀:“九子斜排,上下对易,左右相更,四维挺出”,即可得出结论;
(2)按照口诀:“九子斜排,上下对易,左右相更,四维挺出”,即可得出结论;
(3)根据已知,算出该9个连续自然数,按照口诀:“九子斜排,上下对易,左右相更,四维挺出”,即可得出结论;
(4)按照口诀:“九子斜排,上下对易,左右相更,四维挺出”,即可得出结论.
解答 解:(1)按照口诀:“九子斜排,上下对易,左右相更,四维挺出”
得出方格1:
| -8 | -18 | -4 |
| -6 | -10 | -14 |
| -16 | -2 | -12 |
| 8 | 10 | 6 |
| 6 | 8 | 10 |
| 10 | 6 | 8 |
| 19 | 24 | 17 |
| 18 | 20 | 22 |
| 23 | 16 | 21 |
| 0 | 5 | -2 |
| -1 | 1 | 3 |
| 4 | -3 | 2 |
点评 本题考查了一元一次方程的应用以及构造三阶幻方方法---杨辉法的应用,解题的关键是读懂题意,按照口诀一步步的变换.本题属于中档题型,有点难度,解题过程中有巧妙的办法,即利用给定的例题,再找出所以填写的9个数的中位数,看二者相差多少,再去给定的四维挺出表格中做相应的变动即可.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:选择题
 如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠BAC=50°,则∠AEC的度数为( )
如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠BAC=50°,则∠AEC的度数为( )| A. | 65° | B. | 75° | C. | 50° | D. | 55° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,方格纸中的每个小方格都是边长为1的正方形,△ABC的顶点均在格点上.
如图,方格纸中的每个小方格都是边长为1的正方形,△ABC的顶点均在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 内切 | B. | 外切 | C. | 相交 | D. | 内含 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
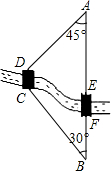 如图所示,A、B两地之间有一条河,原来从A地到B地需要经过桥DC,沿折线A→D→C→B到达,现在新建了桥EF(EF=DC),可直接沿直线AB从A地到达B地,已知BC=12km,∠A=45°,∠B=30°,桥DC和AB平行.
如图所示,A、B两地之间有一条河,原来从A地到B地需要经过桥DC,沿折线A→D→C→B到达,现在新建了桥EF(EF=DC),可直接沿直线AB从A地到达B地,已知BC=12km,∠A=45°,∠B=30°,桥DC和AB平行.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com