
【题目】在一条不完整的数轴上从左到右有点A,B,C,其中点A到点B的距离为3,点C到点B的距离为7,如图所示:设点A,B,C所对应的数的和是m.
![]()
(1)若以C为原点,则m的值是_______;
(2)若原点0在图中数轴上,且点C到原点0的距离为4,求m的值;
(3)动点P从A点出发,以每秒2个单位长度的速度向终点C移动,动点Q同时从B点出发,以每秒1个单位的速度向终点C移动,当几秒后,P、Q两点间的距离为2?(直接写出答案即可)
【答案】(1)-17;(2)m=-5或-29;(3)当1秒或5秒后,P、Q两点间的距离为2.
【解析】
(1)根据已知点A到点B的距离为3和点C到点B的距离为7求出即可;
(2)分为两种情况,当O在C的左边时,当O在C的右边时,求出每种情况A、B、C对应的数,即可求出m;
(3)分为两种情况,当P在Q的左边时,当P在Q的左边时,假如C为原点,求出P、Q对应的数,列出算式,即可求出t.
(1)当以C为原点时,A、B对应的数分别为-7,-10,m=-10+(-7)+0=-17,
故答案为:7,-17;
(2)当O在C的左边时,A、B、C三点在数轴上所对应的数分别为-6、-3、4,
则m=-6-3+4=-5,
当O在C的右边时,A、B、C三点在数轴上所对应的数分别为-14、-11、-4,
则m=-14-11-4=-29,
综上所述:m=-5或-29;
(3)假如以C为原点,则A、B、C对应的数为-10,-7,0,Q对应的数是-(7-t),P对应的数是-(10-2t),
当P在Q的左边时,[-(7-t)]-[-(10-2t)]=2,
解得:t=1,
当P在Q的左边时,[-(10-2t)]-[-(7-t)]=2,
解得:t=5,
即当1秒或5秒后,P、Q两点间的距离为2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两列火车分别从A、B两城同时匀速驶出,甲车开往B城,乙车开往A城.由于墨迹遮盖,图中提供的是两车距B城的路程S甲(千米)、S乙(千米)与行驶时间t(时)的函数图象的一部分.
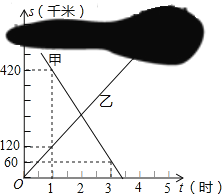
(1)分别求出S甲、S乙与t的函数关系式(不必写出t的取值范围);
(2)求A、B两城之间的距离,及t为何值时两车相遇;
(3)当两车相距300千米时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=0.5千米,则该沙田的面积为________________平方千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
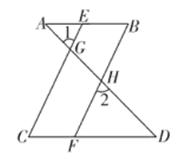
【题目】如图,已知![]() ,
,![]() ,问:
,问:![]() 与
与![]() 平行吗?请说明理由.
平行吗?请说明理由.
解:![]() .理由如下:
.理由如下:
∵![]() (已知)
(已知)
![]() ( )
( )
∴![]() _____________
_____________
∴![]() ( )
( )
![]() _________
_________![]() ( )
( )
又∵![]() ( )
( )
∴∠_________![]()
∴![]() ( )
( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在正方形ABCD中,![]() ,点E,F分别在BC、CD上,
,点E,F分别在BC、CD上,![]() ,试探究
,试探究![]() 面积的最小值。
面积的最小值。
下面是小丽的探究过程:
(1)延长EB至G,使![]() ,连接AG,可以证明
,连接AG,可以证明![]() .请完成她的证明;
.请完成她的证明;
(2)设![]() ,
,![]() ,
,![]()
①结合(1)中结论,通过计算得到![]() 与x的部分对应值。请求出表格中a的值:(写出解答过程)
与x的部分对应值。请求出表格中a的值:(写出解答过程)
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 10 | 8.18 | 6.67 | 5.38 | 4.29 | 3.33 | a | 1.76 | 1.11 | 0.53 | 0 |
②利用上表和(1)中的结论通过描点、连线可以分别画出函数![]() 、
、![]() 的图像、请在图②中完善她的画图;
的图像、请在图②中完善她的画图;
③根据以上探究,估计![]() 面积的最小值约为(结果估计到0.1)。
面积的最小值约为(结果估计到0.1)。


图① 图②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;乙车匀速前往A地,设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数图象如图所示
(1)求甲车从A地到达B地的行驶时间;
(2)求甲车返回时y与x之间的函数关系式,并写出自变量x的取值范围;
(3)求乙车到达A地时甲车距A地的路程.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com