
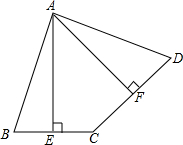
 如图,在四边形ABCD中,点E是BC的中点,点F是CD的中点,且AE⊥BC,AF⊥CD.
如图,在四边形ABCD中,点E是BC的中点,点F是CD的中点,且AE⊥BC,AF⊥CD.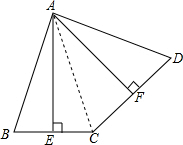 (1)证明:如图,连接AC,
(1)证明:如图,连接AC,
|


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
a±2
|
| b |
| b |
a±2
|
3±2
|
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
3+2
|
(1+
|
| 2 |
5+2
|
7-
|
查看答案和解析>>
科目:初中数学 来源: 题型:
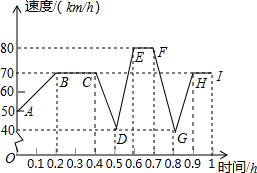 平川四中教生物的王老师驱车到屈吴山采集植物标本,在上山行驶过程中,要经过上坡、下坡、平路等路段,她的SUV在自身动力不变的情况下,上坡时速度越来越慢,下坡时速度越来越快,平路上保持匀速行驶,下面的图象表示了她开车在山区行驶过程中的速度随时间变化的情况.
平川四中教生物的王老师驱车到屈吴山采集植物标本,在上山行驶过程中,要经过上坡、下坡、平路等路段,她的SUV在自身动力不变的情况下,上坡时速度越来越慢,下坡时速度越来越快,平路上保持匀速行驶,下面的图象表示了她开车在山区行驶过程中的速度随时间变化的情况.查看答案和解析>>
科目:初中数学 来源: 题型:
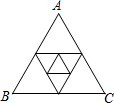 如图,△ABC的三边长分别为a,b,c,以它的三边中点为顶点组成一个新三角形,以这个新三角形三边中点为顶点又组成一个小三角形,求这个小三角形的周长.
如图,△ABC的三边长分别为a,b,c,以它的三边中点为顶点组成一个新三角形,以这个新三角形三边中点为顶点又组成一个小三角形,求这个小三角形的周长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com