
| A. | ①② | B. | ②③ | C. | ③④ | D. | ②③④ |
分析 用加减法解出方程组,根据方程组的解对各个选项进行判断即可.
解答 解:$\left\{\begin{array}{l}{x+y=1-a①}\\{x-y=3a+5②}\end{array}\right.$
①+②得,x=3+a,
①-②得,y=-2a-2,
①由题意得,3+a>0,a>-3,
-2a-2≥0,a≤-1,
∴-3<a≤-1,①不正确;
②3+a=-2a-2,a=-$\frac{5}{3}$,②正确;
③a=-2时,x+y=1-a=3,5+a=3,③正确;
④x≤1时,-3<a≤-2,则4>-2a-2≥2,④错.
故选:B.
点评 本题考查的是二元一次方程组的解法和一元一次不等式的解法,正确解出方程组是解题的关键,注意方程与不等式的综合运用.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:解答题
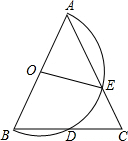 如图,以△ABC一边AB为直径作半圆,与另外两边分别交于点D、E,且点D为BC的中点.
如图,以△ABC一边AB为直径作半圆,与另外两边分别交于点D、E,且点D为BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-x-y)(-y+x)=-x2-y2 | B. | x2-2x-3=(x-1)2-4 | C. | $1-\frac{1}{x}=x-1$ | D. | (x-y)-1=y-x |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com