
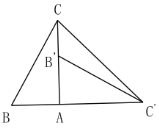
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 可以由
可以由![]() 绕点
绕点![]() 顺时针旋转90°得到(点
顺时针旋转90°得到(点![]() 与点
与点![]() 是对应点,点
是对应点,点![]() 与点
与点![]() 是对应点),连接
是对应点),连接![]() ,则
,则![]() 的度数是________.
的度数是________.
【答案】15°
【解析】
先根据三角形内角和计算出∠ACB=90°60°=30°,由于△AB′C′由△ABC绕点A顺时针旋转90°得到,根据旋转的性质得到AC′=AC,∠C′AB′=∠CAB=90°,则△ACC′为等腰直角三角形,得到∠AC′C=45°,然后利用∠CC′B′=∠AC′C∠AC′B′计算即可.
解:∵∠BAC=90°,∠B=60°,
∴∠ACB=90°60°=30°,
∵△AB′C′由△ABC绕点A顺时针旋转90°得到,
∴AC′=AC,∠C′AB′=∠CAB=90°,∠AC′B′=30°,
∴△ACC′为等腰直角三角形,
∴∠AC′C=45°,
∴∠CC′B′=∠AC′C∠AC′B′=45°30°=15°.
故答案为15°.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 是两座现代化城市,
是两座现代化城市,![]() 是一个古城遗址,
是一个古城遗址,![]() 城在
城在![]() 城的北偏东
城的北偏东![]() ,在
,在![]() 城的北偏西
城的北偏西![]() ,
,![]() 城在
城在![]() 城的正东方向,且
城的正东方向,且![]() 城与
城与![]() 城相距120千米,现在
城相距120千米,现在![]() 、
、![]() 两城市修建一条笔直的高速公路.
两城市修建一条笔直的高速公路.
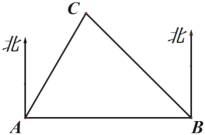
(1)请你计算公路![]() 的长度(结果保留根号);
的长度(结果保留根号);
(2)若以![]() 为圆心,以60千米为半径的圆形区域内为古迹和地下文物保护区,请你分析公路
为圆心,以60千米为半径的圆形区域内为古迹和地下文物保护区,请你分析公路![]() 会不会穿越这个保护区,并说明理由.
会不会穿越这个保护区,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,点B位于(4,0)、(5,0)之间,与y轴交于点C,对称轴为直线x=2,直线y=﹣x+c与抛物线y=ax2+bx+c交于C,D两点,D点在x轴上方且横坐标小于5,则下列结论:①4a+b+c>0;②a﹣b+c<0;③m(am+b)<4a+2b(其中m为任意实数);④a<﹣1,其中正确的是( )

A.①②③④B.①②③C.①②④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学社团成员想利用所学的知识测量某广告牌的宽度![]() 图中线段MN的长
图中线段MN的长![]() ,直线MN垂直于地面,垂足为点
,直线MN垂直于地面,垂足为点![]() 在地面A处测得点M的仰角为
在地面A处测得点M的仰角为![]() 、点N的仰角为
、点N的仰角为![]() ,在B处测得点M的仰角为
,在B处测得点M的仰角为![]() ,
,![]() 米,且A、B、P三点在一直线上
米,且A、B、P三点在一直线上![]() 请根据以上数据求广告牌的宽MN的长.
请根据以上数据求广告牌的宽MN的长.
![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 交
交![]() 轴于点
轴于点![]() 、
、![]() (
(![]() 左
左![]() 右),交
右),交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,
,![]() .
.
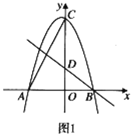
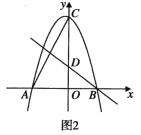
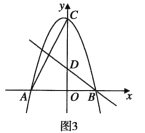
(1)求![]() 、
、![]() 的值;
的值;
(2)点![]() 是第三象限抛物线上的任意一点,设点
是第三象限抛物线上的任意一点,设点![]() 的横坐标为
的横坐标为![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数解析式(不要求写出自变量
的函数解析式(不要求写出自变量![]() 的取值范围);
的取值范围);
(3)在(2)的条件下,连接![]() 、
、![]() ,当
,当![]() 平分
平分![]() 时,以线段
时,以线段![]() 为边,在
为边,在![]() 上方作等边
上方作等边![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 内接于⊙
内接于⊙![]() ,直径
,直径![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() .过点
.过点![]() 作⊙
作⊙![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() .
.
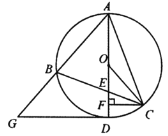
(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)若![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,连接![]() ,设
,设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,若
,若![]() ,求
,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某排球队6名场上队员的身高(单位:cm)是:180,184,188,190,192,194.现用一名身高为186cm的队员换下场上身高为192cm的队员,与换人前相比,场上队员的身高( )
A. 平均数变小,中位数变小
B. 平均数变小,中位数变大
C. 平均数变大,中位数变小
D. 平均数变大,中位数变大
查看答案和解析>>
科目:初中数学 来源: 题型:
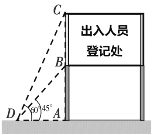
【题目】2020春节期间,为了进一步做好新型冠状病毒感染的肺炎疫情防控工作,防止新型肺炎外传,切断传播途径.项城市市区各入口一些主要路段均设立了检测点,对出入人员进行登记和体温检测。下图为一关口的警示牌,已知立杆AB高度是3m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°.求警示牌BC的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com