
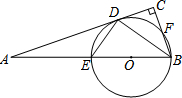
 已知:如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于点D,经过B、D两点的⊙O交AB 于点E,交BC于点F,EB为⊙O的直径.
已知:如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于点D,经过B、D两点的⊙O交AB 于点E,交BC于点F,EB为⊙O的直径.| 1 |
| 3 |
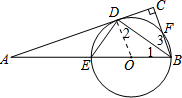 (1)证明:如图,连结OD.
(1)证明:如图,连结OD.| 1 |
| 3 |
| BC |
| cos∠ABC |
| OD |
| BC |
| AO |
| AB |
| r |
| 2 |
| 6-r |
| 6 |
| 3 |
| 2 |
| 3 |
| 2 |


科目:初中数学 来源: 题型:
| 1 |
| 2 |
| A、y1>y2 |
| B、y1<y2 |
| C、y1=y2 |
| D、无法比较 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| 3 |
| 2 |
| 9 |
| 2x+1 |
| 6 |
| 2x-1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
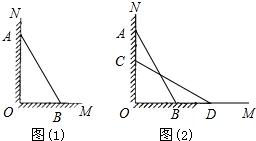 如图(1),一架长为20米云梯AB斜靠在竖直的墙ON上,这时云梯下端B到墙底端O的距离BO=12米,在下列结论中,正确的是( )
如图(1),一架长为20米云梯AB斜靠在竖直的墙ON上,这时云梯下端B到墙底端O的距离BO=12米,在下列结论中,正确的是( )A、当消防员爬到距离地面
| ||
| B、如图(2),当梯子顶端A沿墙下滑3米时,底端B向外移动3米 | ||
| C、如图(2),在梯子下滑过程中,梯子AB与墙ON,地面OM构成的三角形面积存在最大值,最大值为100米2 | ||
D、若在射线ON上存在一点G,使得△ABG为等腰三角形,则AG=
|
查看答案和解析>>
科目:初中数学 来源: 题型:
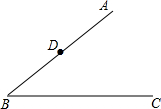 如图,∠ABC的边AB上有一点D.请按下列要求画图并回答问题:
如图,∠ABC的边AB上有一点D.请按下列要求画图并回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:
| A、a<m<n<b |
| B、a<m<b<n |
| C、m<a<b<n |
| D、m<a<n<b |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,扇形折扇完全打开后,如果张开的角度(∠BAC)为120°,骨柄AB的长为30cm,扇面的宽度BD的长为20cm,那么这把折扇的扇面面积为( )
如图,扇形折扇完全打开后,如果张开的角度(∠BAC)为120°,骨柄AB的长为30cm,扇面的宽度BD的长为20cm,那么这把折扇的扇面面积为( )A、
| ||
B、
| ||
C、
| ||
| D、300πcm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com