
【题目】为了提高学生体育中考成绩,某学校打算购买A,B品牌实心球用于学生训练,若一次购买A品牌10个和B品牌5个,需花费350元;若一次购买A品牌4个和B品牌7个,需花费290元.
(1)求A品牌实心球和B品牌实心球的单价.
(2)现学校决定一次性购买A,B品牌实心球共50个,要求A品牌实心球数量不超过B品牌实心球数量的![]() 倍,问如何安排购买方案,使学校购买的总费用最少?最少为多少元?
倍,问如何安排购买方案,使学校购买的总费用最少?最少为多少元?
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过
经过![]() ,
,![]() ,
,![]() 三点.
三点.
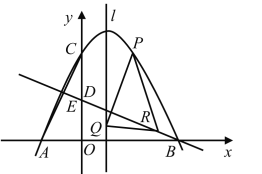
(1)求该抛物线的解析式;
(2)经过点B的直线交y轴于点D,交线段![]() 于点E,若
于点E,若![]() .
.
①求直线![]() 的解析式;
的解析式;
②已知点Q在该抛物线的对称轴l上,且纵坐标为1,点P是该抛物线上位于第一象限的动点,且在l右侧.点R是直线![]() 上的动点,若
上的动点,若![]() 是以点Q为直角顶点的等腰直角三角形,求点P的坐标.
是以点Q为直角顶点的等腰直角三角形,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣![]() x2﹣
x2﹣![]() x+
x+![]() 与x轴交于点A,B(点A在点B的左边),与y轴交于点C,点D是该抛物线的顶点.
与x轴交于点A,B(点A在点B的左边),与y轴交于点C,点D是该抛物线的顶点.
(1)如图1,连接CD,求线段CD的长;
(2)如图2,点P是直线AC上方抛物线上一点,PF⊥x轴于点F,PF与线段AC交于点E;将线段OB沿x轴左右平移,线段OB的对应线段是O1B1,当PE+![]() EC的值最大时,求四边形PO1B1C周长的最小值,并求出对应的点O1的坐标;
EC的值最大时,求四边形PO1B1C周长的最小值,并求出对应的点O1的坐标;
(3)如图3,点H是线段AB的中点,连接CH,将△OBC沿直线CH翻折至△O2B2C的位置,再将△O2B2C绕点B2旋转一周在旋转过程中,点O2,C的对应点分别是点O3,C1,直线O3C1分别与直线AC,x轴交于点M,N.那么,在△O2B2C的整个旋转过程中,是否存在恰当的位置,使△AMN是以MN为腰的等腰三角形?若存在,请直接写出所有符合条件的线段O2M的长;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两种客车,2辆甲种客车与3辆乙种客车的总载客量为180人,1辆甲种客车与2辆乙种客车的总载客量为105人.
(1)请问1辆甲种客车与1辆乙种客车的载客量分别为多少人?
(2)某学校组织240名师生集体外出活动,拟租用甲、乙两种客车共6辆,一次将全部师生送到指定地点.若每辆甲种客车的租金为400元,每辆乙种客车的租金为280元,请给出最节省费用的租车方案,并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为奖励优秀学生,某校准备购买一批文具袋和圆规作为奖品,已知购买1个文具袋和2个圆规需21元,购买2个文具袋和3个圆规需39元.
(1)求文具袋和圆规的单价.
(2)学校准备购买文具袋20个,圆规100个,文具店给出两种优惠方案:
方案一:每购买一个文具袋赠送1个圆规.
方案二:购买10个以上圆规时,超出10个的部分按原价的八折优惠,文具袋不打折.学校选择哪种方案更划算?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)操作发现
如图①,在![]() 中,
中,![]() ,点D是
,点D是![]() 上一点,沿
上一点,沿![]() 折叠
折叠![]() ,使得点C恰好落在
,使得点C恰好落在![]() 上的点E处.则
上的点E处.则![]() 的数量关系为______;
的数量关系为______;![]() ________;
________;
(2)问题解决
如图②,若(1)中![]() ,其他条件不变,请猜想
,其他条件不变,请猜想![]() 之间的关系,并证明你的结论;
之间的关系,并证明你的结论;
(3)类比探究
如图③,在四边形![]() 中,
中,![]() ,连接
,连接![]() ,点E是
,点E是![]() 上一点,沿
上一点,沿![]() 折叠
折叠![]() 使得点D正好落在
使得点D正好落在![]() 上的点F处,若
上的点F处,若![]() ,直接写出
,直接写出![]() 的长.
的长.
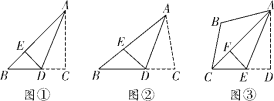
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .
.![]() 是边
是边![]() 的中点,点
的中点,点![]() 为边
为边![]() 上的一个动点(与点
上的一个动点(与点![]() 、
、![]() 不重合),过点
不重合),过点![]() 作
作![]() ,交边
,交边![]() 于点
于点![]() .联结
.联结![]() 、
、![]() ,设
,设![]() .
.
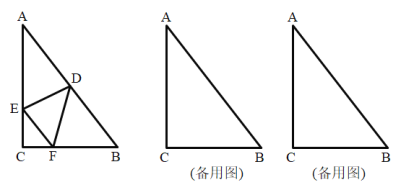
(1)当![]() 时,求
时,求![]() 的面积;
的面积;
(2)如果点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,点
,点![]() 恰好落在边
恰好落在边![]() 上时,求
上时,求![]() 的值;
的值;
(3)以点![]() 为圆心,
为圆心,![]() 长为半径的圆与以点
长为半径的圆与以点![]() 为圆心,
为圆心,![]() 长为半径的圆相交,另一个交点
长为半径的圆相交,另一个交点![]() 恰好落在线段
恰好落在线段![]() 上,求
上,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2019年某中学举行的冬季阳径运动会上,参加男子跳高的15名运动员的成绩如表所示:
成绩(m) | 1.80 | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 |
人数 | 1 | 2 | 4 | 3 | 3 | 2 |
这些运动员跳高成绩的中位数和众数分别是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种成本为每台20元的台灯,规定销售单价不低于成本价,又不高于每台32元.销售中平均每月销售量y(台)与销售单价x(元)的关系可以近似地看做一次函数,如下表所示:
x | 22 | 24 | 26 | 28 |
y | 90 | 80 | 70 | 60 |
(1)请直接写出y与x之间的函数关系式;
(2)为了实现平均每月375元的台灯销售利润,这种台灯的售价应定为多少?这时每月应购进台灯多少个?
(3)设超市每月台灯销售利润为ω(元),求ω与x之间的函数关系式,当x取何值时,ω的值最大?最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com