
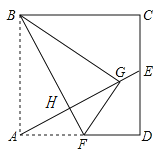
【题目】如图,点F在正方形ABCD的AD边上,连接BF.把△ABF沿BF折叠,与△GBF重合.连接AG并延长交CD于点E,交BF于点H.
(1)证明:BF=AE;
(2)若AB=15,EC=7,求GE的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据正方形的性质和折叠及轴对称的性质证明△ABF≌△DAE,再利用全等三角形的性质即可证明结论;
(2)首先根据△ABF≌△DAE得出![]() ,然后根据正方形的性质和勾股定理求出BF的长度,然后利用
,然后根据正方形的性质和勾股定理求出BF的长度,然后利用![]() 的面积求出AH的长度,进而可求AG的长度,最后利用GE=AE﹣AG即可求解.
的面积求出AH的长度,进而可求AG的长度,最后利用GE=AE﹣AG即可求解.
(1)证明:∵四边形ABCD为正方形,
∴AB=AD,∠BAD=∠D=90°,
由折叠及轴对称的性质可知,△ABF≌△GBF,BF垂直平分AG,
∴BF⊥AE,AH=GH,

∴∠BAH+∠ABH=90°,
又∵∠FAH+∠BAH=90°,
∴∠ABH=∠FAH,
∴△ABF≌△DAE,
∴BF=AE;
(2)解:∵四边形ABCD为正方形,
∴AB=CD=15.
∵CE=7,
∴DE=15﹣7=8.
∵△ABF≌△DAE (已证),
∴AF=DE=8.
在Rt△ABF中,
BF=![]() =17,
=17,
S△ABF=![]() ABAF=
ABAF=![]() BFAH,
BFAH,
∴15×8=17AH,
∴AH=![]() ,
,
∴AG=2AH=![]() ,
,
∵AE=BF=17,
∴GE=AE﹣AG=17﹣![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,E是CD上一点,动点P从点A出发沿折线AE→EC→CB运动到点B时停止,动点Q从点A沿AB运动到点B时停止,它们的速度均为每秒1cm.如果点P、Q同时从点A处开始运动,设运动时间为x(s),△APQ的面积为ycm2,已知y与x的函数图象如图2所示,以下结论:①AB=5cm;②cos∠AED=![]() ;③当0≤x≤5时,y=
;③当0≤x≤5时,y=![]() ;④当x=6时,△APQ是等腰三角形;⑤当7≤x≤11时,y=
;④当x=6时,△APQ是等腰三角形;⑤当7≤x≤11时,y=![]() .其中正确的有( )
.其中正确的有( )
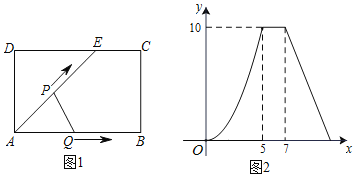
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
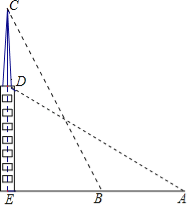
【题目】如图,在一个18米高的楼顶上有一信号塔DC,李明同学为了测量信号塔的高度,在地面的A处测的信号塔下端D的仰角为30°,然后他正对塔的方向前进了18米到达地面的B处,又测得信号塔顶端C的仰角为60°,CD⊥AB与点E,E、B、A在一条直线上.请你帮李明同学计算出信号塔CD的高度(结果保留整数,![]() ≈1.7,
≈1.7,![]() ≈1.4 )
≈1.4 )
查看答案和解析>>
科目:初中数学 来源: 题型:
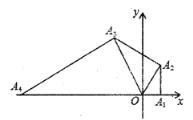
【题目】如图,在平面直角坐标系中,点![]() 的坐标为(1,0),以
的坐标为(1,0),以![]() 为直角边作
为直角边作![]() ,并使
,并使![]() ,再以
,再以![]() 为直角边作
为直角边作![]() ,并使
,并使![]() ,再以
,再以![]() 为直角边作
为直角边作![]() ,并使
,并使![]() ……按此规律进行下去,则点
……按此规律进行下去,则点![]() 的坐标为_________.
的坐标为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠疫情爆发后,各地启动了抗击新冠肺炎的一级应急响应机制,某社区20位90后积极参与社区志愿者工作,充分展示了新时代青年的责任担当,这20位志愿者的年龄统计如表,则他们年龄的众数和中位数分别是( )

A.25岁,25岁B.25岁,26岁C.26岁,25岁D.26岁,26岁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边![]() ,以边
,以边![]() 为直径的半圆与边
为直径的半圆与边![]() ,
,![]() 分别交于点
分别交于点![]() 、
、![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,
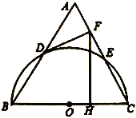
(1)判断![]() 与
与![]() 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(2)过点![]() 作
作![]() 于点
于点![]() ,若等边
,若等边![]() 的边长为8,求
的边长为8,求![]() ,
,![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学准备随机选出七、八、九三个年级各1名学生担任学校国旗升旗手.现已知这三个年级每个年级分别选送一男、一女共6名学生作为备选人.
(1)请你利用树状图或表格列出所有可能的选法;
(2)求选出“一男两女”三名国旗升旗手的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对本校初2017届500名学生中中考参加体育加试测试情况进行调查,根据男生1000米及女生800米测试成绩整理,绘制成不完整的统计图,(图①,图②),请根据统计图提供的信息,回答下列问题:
(1)该校毕业生中男生有 人;扇形统计图中a= ;

(2)补全条形统计图;
(3)若500名学生中随机抽取一名学生,这名学生该项成绩在8分及8分以下的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,EF,EB是⊙O的弦,且EF=EB,EF与AB交于点C,连接OF,若∠AOF=40°,则∠F的度数是( )
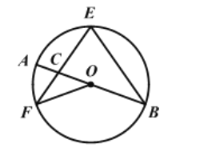
A.20°B.35°C.40°D.55°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com