Question

10．如图，在直角坐标系中，⊙P沿着x轴，绕它的圆心P向原点方向滚动，当⊙P旋转2周时，⊙P与y轴相交于点（0，2）和（0，8），则⊙P开始滚动时圆心的坐标是（40π+4，5）．

Answer 1

分析 与y轴相交（0，2）和（0，8）时，圆心P'作P'C⊥AB于点C，过P作P'D⊥x轴于点D，由切线的性质可求得P'D的长，则可得PB的长，由垂径定理可求得CB的长，在Rt△P'BC中，由勾股定理可求得P'C的长，从而可求得P'点坐标，进而得出点P的纵坐标，最后确定点P的横坐标．

解答 解：如图，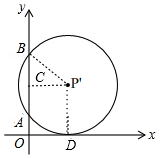

过P'作P'C⊥AB于点C，过P'作P'D⊥x轴于点D，连接P'B，
∵P'为圆心，
∴AC=BC，
∵A（0，2），B（0，8），
∴AB=8-2=6，
∴AC=BC=3，
∴OC=8-3=5，
∵⊙P'与x轴相切，
∴P'D=P'B=OC=5，
在Rt△P'BC中，由勾股定理可得P'C=$\sqrt{P{B}^{2}-B{C}^{2}}$=4，
∴P'点坐标为（4，5），
∴⊙P的半径为5，
∵⊙P旋转2周，
∴滚动的距离为2×2π×5=20π，
∴P（40π+4，5）
故答案为（40π+4，5）．

点评 本题主要考查切线的性质和垂径定理，利用切线的性质求得圆的半径是解题的关键．