
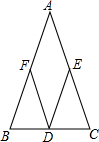
 已知:如图,等腰△ABC中,AB=AC,D是BC的中点,DE∥AB,DF∥AC,求证:四边形AFDE是菱形.
已知:如图,等腰△ABC中,AB=AC,D是BC的中点,DE∥AB,DF∥AC,求证:四边形AFDE是菱形. 科目:初中数学 来源: 题型:解答题
 观察图,先填空,然后回答问题:
观察图,先填空,然后回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,把长方形纸片ABCD沿EF折叠后,点D与点B重合,点C落在点C'的位置上,若∠1=60°,AE=1.
已知:如图,把长方形纸片ABCD沿EF折叠后,点D与点B重合,点C落在点C'的位置上,若∠1=60°,AE=1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为纪念爱国诗人屈原,我市在俯南河隆重举行了一次龙舟比赛,如图是甲、乙两支龙舟队在比赛时的路程s(米)与时间t(分钟)之间的图象,请你根据图象回答下列问题:
为纪念爱国诗人屈原,我市在俯南河隆重举行了一次龙舟比赛,如图是甲、乙两支龙舟队在比赛时的路程s(米)与时间t(分钟)之间的图象,请你根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知四边形ABCD是正方形,△AEF是等边三角形,E、F分别位于DC边和BC边上.
如图,已知四边形ABCD是正方形,△AEF是等边三角形,E、F分别位于DC边和BC边上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了响应国家号召:绿色环保,节约能量.小刚在家屋顶安装了一台太阳能热水器,其横截面积如图所示,已知集热管AE与支架BF所在直线相交于水箱横截面⊙O的圆心O,⊙O的半径为0.2m,AO与屋面AB的夹角为32°,与铅垂线OD的夹角为40°,BF⊥AB于B,OD⊥AD于D,AB=2m,求小刚家屋面AB的坡度和支架BF的长.
为了响应国家号召:绿色环保,节约能量.小刚在家屋顶安装了一台太阳能热水器,其横截面积如图所示,已知集热管AE与支架BF所在直线相交于水箱横截面⊙O的圆心O,⊙O的半径为0.2m,AO与屋面AB的夹角为32°,与铅垂线OD的夹角为40°,BF⊥AB于B,OD⊥AD于D,AB=2m,求小刚家屋面AB的坡度和支架BF的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com