练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    ．如图，AB∥CD，点E在BC上，且CD=CE，∠D=74°，则∠B的度数为（　　）

    A．68°   B．32°    C．22°   D．16°


    B【考点】平行线的性质；等腰三角形的性质．

    【分析】根据等腰三角形两底角相等求出∠C的度数，再根据两直线平行，内错角相等解答即可．

    【解答】解：∵CD=CE，

    ∴∠D=∠DEC，

    ∵∠D=74°，

    ∴∠C=180°﹣74°×2=32°，

    ∵AB∥CD，

    ∴∠B=∠C=32°．

    故选B．

    【点评】本题考查了两直线平行，内错角相等的性质，等腰三角形两底角相等的性质，熟记性质是解题的关键．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    下列计算中，正确的是（     ）

         A. a3•a3=a9          B. 3a3÷2a=a3           C. (a2)3=a6        D. 2a+3a2=5a3

    查看答案和解析>>

    科目：初中数学 来源： 题型：


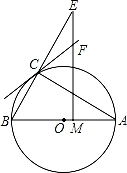
    如图，⊙O是△ABC的外接圆，圆心O在AB上，且∠B=2∠A，M是OA上一点，过M作AB的垂线交AC于点N，交BC的延长线于点E，直线CF交EN于点F，EF=FC．

    （1）求证：CF是⊙O的切线．

    （2）设⊙O的半径为2，且AC=CE，求AM的长．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


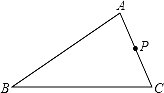
    如图所示，在△ABC中，AB=6，AC=4，P是AC的中点，过P点的直线交AB于点Q，若以A、P、Q为顶点的三角形和以A、B、C为顶点的三角形相似，则AQ的长为　　　　　　．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


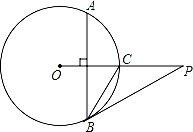
    如图，已知点P是⊙O外一点，PO交圆O于点C，OC=2，AB⊥OC，劣弧AB的度数为120°，连接PB．

    （1）求征：OC=BC；

    （2）当PB的长是多少时，PB是⊙O的切线？写出证明过程．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    分式方程的解是　　　　　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    先化简÷（a+2）+，再求值，a为整数且﹣2≤a≤2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，AB是半圆的直径，点D是的中点，∠ABC=50°，则∠DAB等于（　　）

    A．55°   B．60°    C．65°   D．70°

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


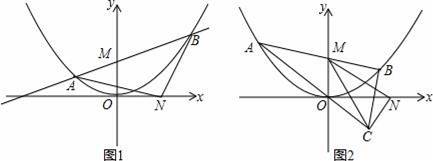
    如图1，动直线l：y=kx+2交抛物线y=x2于A、B两点（A在B的左边），交y轴于M点，N为x轴正半轴上一点，且ON=OM+1

    （1）直接写出M、N两点的坐标

    （2）如图1，连AN、BN，当∠ANB=90°时，求k的值；如图2，过B作y轴的平行线交直线OA于C，试探求△MNC的周长的最小值．

    　

    　


    查看答案和解析>>

    同步练习册答案