
【题目】已知直线AB∥CD,直线EF与AB,CD分别相交于点E,F.

(1)如图1,若∠1=60°,求∠2=__________;∠3=__________.
(2)若点P是平面内的一个动点,连结PE,PF,探索∠EPF,∠PEB,∠PFD三个角之间的关系.
①当点P在图2的位置时,可得∠EPF=∠PEB+∠PFD. 理由如下:
如图2,过点P作MN∥AB,则∠EPM=∠PEB(__________)
∵AB∥CD(已知) MN∥AB(作图)
∴MN∥CD(__________)
∴∠MPF=∠PFD (__________)
∴__________+__________=∠PEB+∠PFD(等式的性质)
即:∠EPF=∠PEB+∠PFD.请补充完整说理过程(填写理由或数学式)
②当点P在图3的位置时,此时∠EPF=80°,∠PEB=156°,则∠PFD=__________;
③当点P在图4的位置时,写出∠EPF,∠PEB,∠PFD三个角之间的关系并证明(每一步必须注明理由).
【答案】(1)∠2=60°;∠3=60°;(2)①两直线平行,内错角相等;如果两条直线都和第三条直线平行,那么这两条直线也互相平行;两直线平行,内错角相等;∠EPM+∠FPM;②124°;③∠EPF+∠PFD=∠PEB;证明见解析
【解析】
(1)根据对顶角相等求∠2,根据两直线平行,同位角相等求∠3;
(2)①过点P作MN//AB,根据平行线的性质得∠EPM=∠PEB,且有MN//CD,所以∠MPF=∠PFD,然后利用等式性质易得∠EPF=∠PEB十∠PFD;
②同①;
③利用平行线的性质和三角形的外角性质得到三个角之间的关系.
解:(1)应填∠2=60°,∠3=60°.理由是:
∵∠2=∠1,∠1=60°,
∴∠2=60°,
∵AB//CD
∴∠3=∠1=60°;
(2)①当点P在图(2)的位置时,可得∠EPF=∠PEB+∠PFD. 理由如下:
如图2,过点P作MN∥AB,则∠EPM=∠PEB(两直线平行,内错角相等)
∵AB∥CD(已知),MN∥AB(作图)
∴MN∥CD(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠MPF=∠PFD (两直线平行,内错角相等)
∴ ∠EPM+∠FPM =∠PEB+∠PFD(等式的性质)
即:∠EPF=∠PEB+∠PFD
故答案为:两直线平行,内错角相等;如果两条直线都和第三条直线平行,那么这两条直线也互相平行;两直线平行,内错角相等;∠EPM+∠MP
②当点P在图3的位置时,此时∠EPF=80°,∠PEB=156°,则∠PFD=124°.理由为:
如图3所示,过点P作PM∥AB,
则∠PEB+∠EPM=180°,∠MPF+∠PFD=180°,
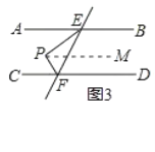
∴∠PEB+∠EPM+∠MPF+∠PFD=180°+180°=360°,即∠EPF+∠PEB+∠PFD=360°
∴∠PFD=360°-80°-156°=124°;
故答案为:124°
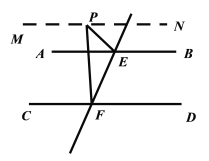
③当点P在图4的位置时,∠EPF,∠PEB,∠PFD三个角之间关系是:
∠EPF+∠PFD=∠PEB
证明如下:
如图4,过点P作MN∥AB,则∠EPM=∠PEB(两直线平行,内错角相等)
∵AB∥CD(已知),MN∥AB,
∴MN∥CD(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠MPF=∠PFD(两直线平行,内错角相等)
∴∠EPM-∠MPF=∠PEB-∠PFD(等式的性质)
即∠EPF+∠PFD=∠PEB


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
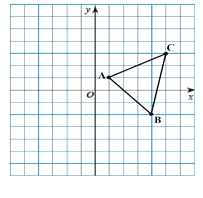
【题目】如图,在平面直角坐标系中, ABC 三个顶点的坐标分别为 A(1,1) , B(4, 2) ,C (5, 3) .
(1)在图中画出 ABC 关于 y 轴的对称 图形 A1B1C1 ;(要求:画出三角形,标出相应顶点的 字母,不写结论)
(2)分别写出A1B1C1 三个顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G,若∠BAC=100°,则∠EAG=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,画![]() ,并画
,并画![]() 的平分线
的平分线![]() .
.
(1)将三角尺的直角顶点落在![]() 的任意一点P上,使三角尺的两条直角边与
的任意一点P上,使三角尺的两条直角边与![]() 的两边分别垂直,垂足为E、F(如图1),则
的两边分别垂直,垂足为E、F(如图1),则![]()
![]() (选填<,>,=)
(选填<,>,=)

(2)把三角尺绕着点P旋转(如图2),![]() 与
与![]() 相等吗?试猜想
相等吗?试猜想![]() 、
、![]() 的大小关系,并说明理由.
的大小关系,并说明理由.
拓展延伸1:在(2)条件下,过点P作直线![]() ,分别交
,分别交![]() 、
、![]() 于点G、H,如图3
于点G、H,如图3
①图中全等三角形有多少对(不添加辅助线)
②猜想![]() 、
、![]() 、
、![]() 之间的关系,并证明你的猜想.
之间的关系,并证明你的猜想.
拓展延伸2:
画![]() ,并画
,并画![]() 的平分线
的平分线![]() ,在
,在![]() 上任取一点P,作
上任取一点P,作![]() .
.![]() 的两边分别与
的两边分别与![]() 、
、![]() 相交于E、F两点(如图4),
相交于E、F两点(如图4),![]() 与
与![]() 相等吗?请说明理由.
相等吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两地间仅有一长为180千米的平直公路,若甲,乙两车分别从A,B两地同时出发匀速前往B,A两地,乙车速度是甲车速度的![]() 倍,乙车比甲车早到45分钟.
倍,乙车比甲车早到45分钟.
(1)求甲车速度;
(2)乙车到达A地停留半小时后以来A地时的速度匀速返回B地,甲车到达B地后立即提速匀速返回A地,若乙车返回到B地时甲车距A地不多于30千米,求甲车至少提速多少千米/时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】铁岭“荷花节”举办了为期15天的“荷花美食”厨艺秀.小张购进一批食材制作特色美食,每盒售价为50元,由于食材需要冷藏保存,导致成本逐日增加,第x天(1≤x≤15且x为整数)时每盒成本为p元,已知p与x之间满足一次函数关系;第3天时,每盒成本为21元;第7天时,每盒成本为25元,每天的销售量为y盒,y与x之间的关系如下表所示:
第x天 | 1≤x≤6 | 6<x≤15 |
每天的销售量y/盒 | 10 | x+6 |
(1)求p与x的函数关系式;
(2)若每天的销售利润为w元,求w与x的函数关系式,并求出第几天时当天的销售利润最大,最大销售利润是多少元?
(3)在“荷花美食”厨艺秀期间,共有多少天小张每天的销售利润不低于325元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边![]() 内一点
内一点![]() 将
将![]() 绕点C按顺时针方向旋转
绕点C按顺时针方向旋转![]() 得
得![]() ,连接
,连接![]() 已知
已知![]()
![]() .
.
![]() 求证:
求证:![]() 是等边三角形;
是等边三角形;
![]() 当
当![]() 时,试判断
时,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 探究:当
探究:当![]() 为多少度时,
为多少度时,![]() 是等腰三角形.
是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
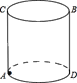
【题目】如图,圆柱的高为![]() ,底面半径为
,底面半径为![]() ,在圆柱下底面的
,在圆柱下底面的![]() 点处有一只蚂蚁,它想吃到上底面
点处有一只蚂蚁,它想吃到上底面![]() 处的食物,已知四边形
处的食物,已知四边形![]() 的边
的边![]() 、
、![]() 恰好是上、下底面的直径.为:蚂蚁至少要爬行多少路程才能食到食物?
恰好是上、下底面的直径.为:蚂蚁至少要爬行多少路程才能食到食物?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com