
分析 (1)已知抛物线上三点坐标,代入一般式,列三元一次方程组,求a、b、c的值,确定抛物线解析式,再求抛物线与y轴交点的纵坐标.
(2)由于已知抛物线与x轴的交点坐标,则可设交点式y=a(x+$\frac{1}{2}$)(x-$\frac{3}{2}$),然后把点(0,-5)代入求出a即可.
解答 解:(1)把(-3,2),(-1,-1),(1,3)代入抛物线解析式,得$\left\{\begin{array}{l}{9a-3b+c=2}\\{a-b+c=-1}\\{a+b+c=3}\end{array}\right.$
解得$\left\{\begin{array}{l}{a=\frac{7}{8}}\\{b=2}\\{c=\frac{1}{8}}\end{array}\right.$
∴该函数的解析式为:y=$\frac{7}{8}$x2+2x+$\frac{1}{8}$.
(2)设抛物线的解析式为y=a(x+$\frac{1}{2}$)(x-$\frac{3}{2}$),
把点(0,-5)代入得a×$\frac{1}{2}$×(-$\frac{3}{2}$)=-5,
解得a=$\frac{20}{3}$,
则y=$\frac{20}{3}$(x+$\frac{1}{2}$)(x-$\frac{3}{2}$)=$\frac{20}{3}$x2-$\frac{20}{3}$x-5.
所以抛物线的解析式为y=$\frac{20}{3}$x2-$\frac{20}{3}$x-5.
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
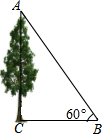 有一棵树较高(如图),无法直接量出它的高度,可以先用测角器在离树底部不远处的地面上找一点B,使此时测得树顶A的仰角为60°,再用皮尺测得BC之间的距离为a,由此你能得出这棵树的高度吗?
有一棵树较高(如图),无法直接量出它的高度,可以先用测角器在离树底部不远处的地面上找一点B,使此时测得树顶A的仰角为60°,再用皮尺测得BC之间的距离为a,由此你能得出这棵树的高度吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
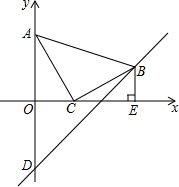 在平面直角坐标系中,现将一块等腰直角三角板ABC放在第一象限,斜靠在两条坐标轴上,且点A(0,2),点C(1,0),BE⊥x轴于点E,一次函数y=x+b经过点B,交y轴于点D.
在平面直角坐标系中,现将一块等腰直角三角板ABC放在第一象限,斜靠在两条坐标轴上,且点A(0,2),点C(1,0),BE⊥x轴于点E,一次函数y=x+b经过点B,交y轴于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com