
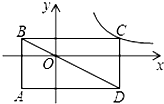
 如图,矩形ABCD的对角线BD经过的坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=
如图,矩形ABCD的对角线BD经过的坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=| k2+4k+1 |
| x |



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
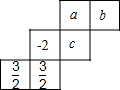 如图,是一个正方体纸盒的表面展开图,在其中的三个正方形a,b,c 内分别填入适当的数,使得折成正方体后相对的面上的两个数满足下列条件:
如图,是一个正方体纸盒的表面展开图,在其中的三个正方形a,b,c 内分别填入适当的数,使得折成正方体后相对的面上的两个数满足下列条件:查看答案和解析>>
科目:初中数学 来源: 题型:
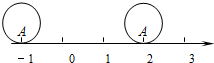 如图,有一个高为6的圆柱体,现在它的底面圆周在数轴上滚动,在滚动前圆柱体底面圆周上有一点A和数轴上表示-1的点重合,当圆柱体滚动一周时A点恰好落在了表示2的点的位置.则这个圆柱体的侧面积是
如图,有一个高为6的圆柱体,现在它的底面圆周在数轴上滚动,在滚动前圆柱体底面圆周上有一点A和数轴上表示-1的点重合,当圆柱体滚动一周时A点恰好落在了表示2的点的位置.则这个圆柱体的侧面积是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com