
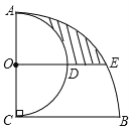
【题目】如图,AC⊥BC,AC=BC=2,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作⊙C,过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是______.
【答案】![]()
【解析】
如图,图中S阴影=S扇形ACB-S扇形AOD-S扇形ECB-S△OCE.根据已知条件易求得OA=OC=OD=2,BC=CE=4.∠ECB=∠OEC=30°,所以由扇形面积公式、三角形面积公式进行解答即可.
如图,连接CE.
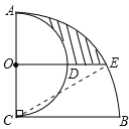
∵AC⊥BC,AC=BC=2,以AC为直径作半圆,圆心为点O;
以点C为圆心,BC为半径作![]() ,
,
∴∠ACB=90°,OA=OC=OD=1,BC=CE=2.
又∵OE∥BC,
∴∠AOE=∠COE=90°.
∴在直角△OEC中,OC=![]() CE,
CE,
∴∠OEC=30°,OE=![]() .
.
∴∠ECB=∠OEC=30°,
∴S阴影=S扇形ACB-S扇形AOD-S扇形ECB-S△OCE
=![]() -
-![]() -
-![]() -
-![]() ×1×
×1×![]()
=![]() π-
π-![]() .
.
故答案为:![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
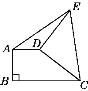
【题目】如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,将腰CD以D为中心逆时针旋转90°至DE,连接AE、CE,△ADE的面积为3,则BC的长为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
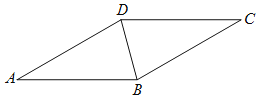
【题目】如图,BD是菱形ABCD的对角线.
(1)请用直尺和圆规作AB的垂直平分线EF,垂足为点E,交AD于点F;(不要求写作法,保留作图痕迹)
(2)在(1)的条件下,连接BF,若∠CBD=75°,求∠DBF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
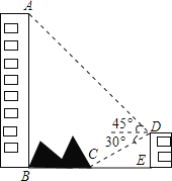
【题目】 如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80m,DE=10m,求障碍物B,C两点间的距离(结果精确到0.1m)(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=BC,P为△ABC内部一点,且∠APB=∠BPC=135°
(1)求证:△PAB∽△PBC
(2)求证:PA=2PC
(3)若点P到三角形的边AB,BC,CA的距离分别为h1,h2,h3,求证h12=h2·h3

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了改善办学条件,计划购置一批电子白板和一批笔记本电脑,经投标,购买1块电子白板比买3台笔记本电脑多3000元,购买4块电子白板和5台笔记本电脑共需80000元.
(1)求购买1块电子白板和一台笔记本电脑各需多少元?
(2)根据该校实际情况,需购买电子白板和笔记本电脑的总数为396,要求购买的总费用不超过2700000元,并购买笔记本电脑的台数不超过购买电子白板数量的3倍,该校有哪几种购买方案?
(3)上面的哪种购买方案最省钱?按最省钱方案购买需要多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两个不透明的布袋里,都装有3个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字0,1,2,乙袋中的小球上分别标有数字﹣1,﹣2,3,现从甲袋中任意摸出一个小球,记其标有的数字为x,再从乙袋中任意摸出一个小球,记其标有的数字为y,以此确定点M的坐标(x,y).
(1)请你用画树状图或列表的方法,写出点M的所有可能的坐标;
(2)求点M(x,y)在函数y=﹣![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
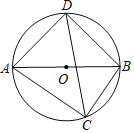
【题目】如图,![]() 是⊙
是⊙![]() 的直径,点
的直径,点![]() 分别在两个半圆上(不与点
分别在两个半圆上(不与点![]() 重合),
重合),![]() 的长分别是关于
的长分别是关于![]() 的方程
的方程![]()
![]() 的两个实数根.
的两个实数根.
(1)![]() 的值为_____;
的值为_____;
(2)连接![]() 三者之间的等量关系为_____.
三者之间的等量关系为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com