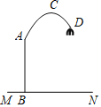
【题目】如图，一款落地灯的灯柱AB垂直于水平地面MN，高度为1.6米，支架部分的形为开口向下的抛物线，其顶点C距灯柱AB的水平距离为0.8米，距地面的高度为2.4 米，灯罩顶端D距灯柱AB的水平距离为1.4米，则灯罩顶端D距地面的高度为______米．
【答案】1.95
【解析】
以点B为原点建立直角坐标系，则点C为抛物线的顶点，即可设顶点式y＝a（x0.8）2＋2.4，点A的坐标为（0，1.6），代入可得a的值，从而求得抛物线的解析式，将点D的横坐标代入，即可求点D的纵坐标就是点D距地面的高度
解：
如图，以点B为原点，建立直角坐标系．
由题意，点A（0，1.6），点C（0.8，2.4），则设顶点式为y＝a（x0.8）2＋2.4
将点A代入得，1.6＝a（00.8）2＋2.4，解得a＝1.25
∴该抛物线的函数关系为y＝1.25（x0.8）2＋2.4
∵点D的横坐标为1.4
∴代入得，y＝1.25×（1.40.8）2＋2.4＝1.95
故灯罩顶端D距地面的高度为1.95米
故答案为1.95.
名校课堂系列答案科目：初中数学 来源： 题型：
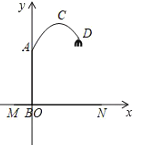
【题目】如图①，窗帘的褶皱是指按照窗户的实际宽度将窗帘布料以一定比例加宽的做法，褶皱之后的窗帘更能彰显其飘逸、灵动的效果．其中，窗宽度的1.5倍为平褶皱，窗宽度的2倍为波浪褶皱．如图②，小莉房间的窗户呈长方形，窗户的宽度（AD）比高度（AB）的少0.5m，某种窗帘的价格为120元/m2．如果以波浪褶皱的方式制作该种窗帘比以平褶皱的方式费用多180元，求小莉房间窗户的宽度与高度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知x1，x2是关于x的一元二次方程x2＋2(m－3) x＋m2＋1＝0的两个根．
（1）当m取何值时，方程有两个不相等的实数根？
（2）若以x1，x2为对角线的菱形边长是
，试求m的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系
中，菱形
的对角线
在
轴上，若菱形的周长为
，点
的坐标为
，反比例函数
的图象经过点
．
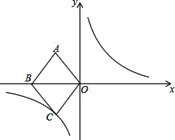
(1)求该反比例函数的解析式；
(2)若点
是反比例函数上的一点，且
的面积恰好等于菱形的面积，求点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
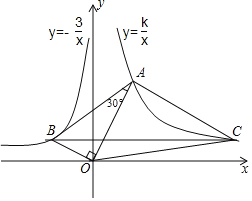
【题目】如图，已知∠AOB=90°，∠OAB=30°，反比例函数
的图象过点
，反比例函数
的图象过点A
（1）求
和
的值.
（2）过点B作BC∥x轴，与双曲线
交于点C，求△OAC的面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两车分别从A、B两地同时出发，在同一条公路上，匀速行驶，相向而行，到两车相遇时停止.甲车行驶一段时间后，因故停车0.5小时，故障解除后，继续以原速向B地行驶，两车之间的路程y（千米）与出发后所用时间x(小时）之间的函数关系如图所示.
（1）求甲、乙两车行驶的速度V甲、V乙.
（2）求m的值.
（3）若甲车没有故障停车，求可以提前多长时间两车相遇.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，已知抛物线
和直线l:y=kx+b，点A(-3,-3)，B(1,-1)均在直线l上．
（1）若抛物线C与直线l有交点，求a的取值范围；
（2）当a=-1，二次函数
的自变量x满足m≤x≤m+2时，函数y的最大值为-4，求m的值；
（3）若抛物线C与线段AB有两个不同的交点，请直接写出a的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，若二次函数y=ax2+bx+c（a≠0）图象的对称轴为x=1，与y轴交于点C，与x轴交于点A、点B（﹣1，0），则
①二次函数的最大值为a+b+c；
②a﹣b+c＜0；
③b2﹣4ac＜0；
④当y＞0时，﹣1＜x＜3，其中正确的个数是（ ）
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线y＝ax2+bx+c上部分点的横坐标x，纵坐标y的对应值如下表：
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知，下列说法中正确的是（ ）
A. 抛物线与x轴的一个交点为（4，0）
B. 函数y＝ax2+bx+c的最大值为6
C. 抛物线的对称轴是x＝
D. 在对称轴右侧，y随x增大而增大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com